NB: per risparmiare
spazio, gli esempi sonori sono stati compressi in MP3. Di conseguenza
la loro qualità è inferiore rispetto a quelli in formato lineare distribuiti nel
corso delle lezioni.
Il primo, del tutto meccanico, è quello della FFT inversa (IFFT). Si tratta di una semplice inversione della FFT, con cui, dai dati dell'analisi, si ricostruisce l'onda che li ha generati.
Dal punto di vista musicale, però, questo sistema non è molto interessante perché non permette di apportare alcuna modifica al suono. La cosa veramente interessante, invece, è la possibilità di effettuare l'analisi, modificare i dati e infine sintetizzare un nuovo suono così elaborato.
E' chiaro che l'elaborazione effettuata sui dati ricavati dalla FFT (cioè nel dominio della frequenza) è molto più raffinata e precisa di quella effettuata sulla forma d'onda (nel dominio del tempo) con programmi come Cool-Edit e simili. Questo perché, nel dominio della frequenza si vanno a modificare dei puri numeri che possono essere cambiati anche singolarmente senza effetti collaterali. Per fare un esempio banale, in un suono basso con molti armonici l'eliminazione di una singola componente senza toccare le altre è quasi impossibile perché un filtro notch (che elimina una banda ed è l'inverso del passa-banda), per quanto stretto, ha sempre qualche effetto anche sulle componenti vicine. Lavorando sui numeri, invece, basta cancellare totalmente quella componente azzerando tutti i suoi valori di ampiezza, senza effetti sulle altre.
Molto bene. In teoria abbiamo un potente sistema di elaborazione del suono, ma dov'è il problema? Come dice uno dei corollari della Legge di Murphy, "c'è sempre un ulteriore disastro". Qui il disastro è costituito dal fatto che tutti quei numeri che noi interpretiamo come componenti, per il computer non significano nulla, ma sono soltanto numeri.
Pensate, per esempio, al sonogramma di un suono con componenti armoniche. Noi vediamo delle linee orizzontali e diciamo "ecco gli armonici", ma il computer non ha un concetto del genere. Non ci arriva nemmeno vicino. Per lui non esiste nemmeno il sonogramma nella sua interezza, ma soltanto un grafico in cui plotta, uno dopo l'altro, i risultati di centinaia di FFT. Siamo noi che, con la nostra capacità di sintesi, diamo un significato al sonogramma.
Il computer non può nemmeno capire, per es., un concetto come "la terza componente" perché lui ha in mano i dati di centinaia di FFT disgiunte in cui la terza componente non è sempre la stessa. In un suono di pianoforte, all'inizio c'è il rumore del martelletto e quindi la terza componente è una di quelle che fanno parte del rumore, mentre a metà nota è effettivamente la seconda armonica. Altro esempio: in un suono vibrato, come può il computer capire che quella frequenza che in una analisi è 2000 Hz, in quella seguente a 2050 Hz e in quella dopo 1990, in realtà sono la stessa componente?
Per lavorare in questo modo è evidentemente necessario un sistema di riduzione dei dati che, oltre a fornire al computer qualche informazione in più, lo aiuti a isolare le componenti importanti e a ricostruire un quadro complessivo coerente.
Questo software cerca e (possibilmente) individua le componenti armoniche di un dato suono (compresa la fondamentale) e produce, per ognuna di esse, una serie di dati che ne descrivono la variazione in frequenza e in ampiezza. Tali dati sono, poi editabili con appositi software e infine vengono passati al modulo adsyn di CSound (ADditive SYNthesis) che esegue la sintesi. Si tratta di sintesi additiva classica perché ogni sinusoide viene generata a parte con i propri inviluppi in ampiezza e in frequenza.
Hetro funziona al meglio su suoni con componenti armoniche o quasi armoniche. Ciò non toglie che possa dare buoni risultati anche con suoni inarmonici, ma solo se le componenti sono ben isolate (NON rumore). Il suo nome, infatti, deriva dal vecchio filtro a eterodina che nella versione digitale è rimpiazzato da un ben più preciso filtro COMB, la cui risposta in frequenza è costituita da una serie di picchi ugualmente distanziati in Hertz e quindi corrispondenti agli armonici di una fondamentale f1, come nella figura seguente.
In tal modo, hetro filtra via ciò che non è almeno in prossimità degli
armonici e poi individua, per ogni banda, la componente più forte. Si
tratta, quindi, di una analisi indirizzata alla ricerca e
all'isolamento delle componenti armoniche, escludendo le componenti
rumoristiche. Grazie a questa semplificazione, hetro 'capisce' il
concetto di componente ed è in grado di seguire ognuna di esse
collegando i risultati delle centinaia di analisi che deve eseguire.
Per lavorare bene, ha bisogno di alcune informazioni:
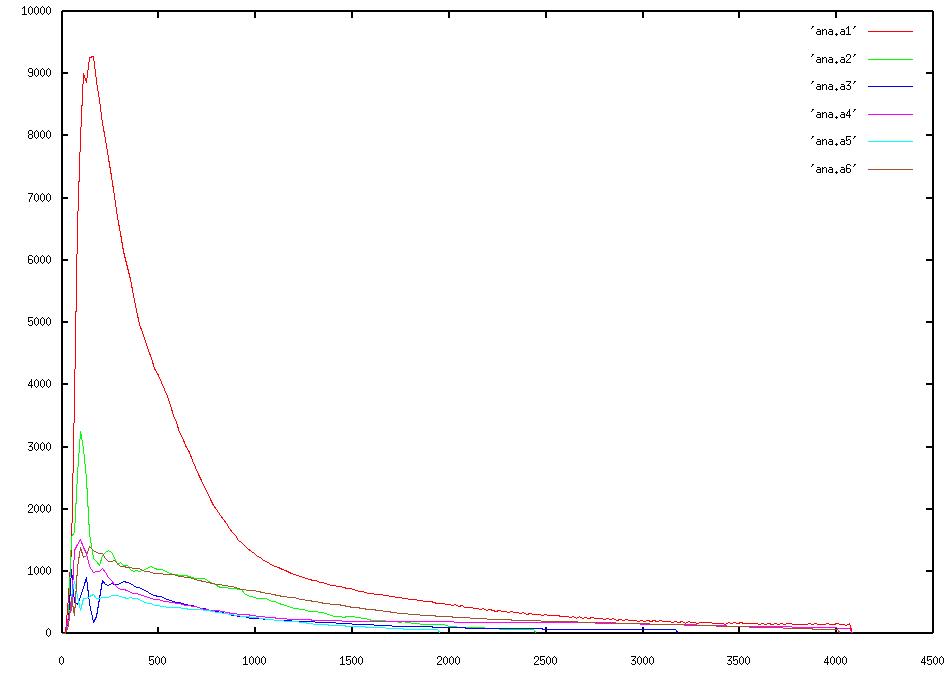
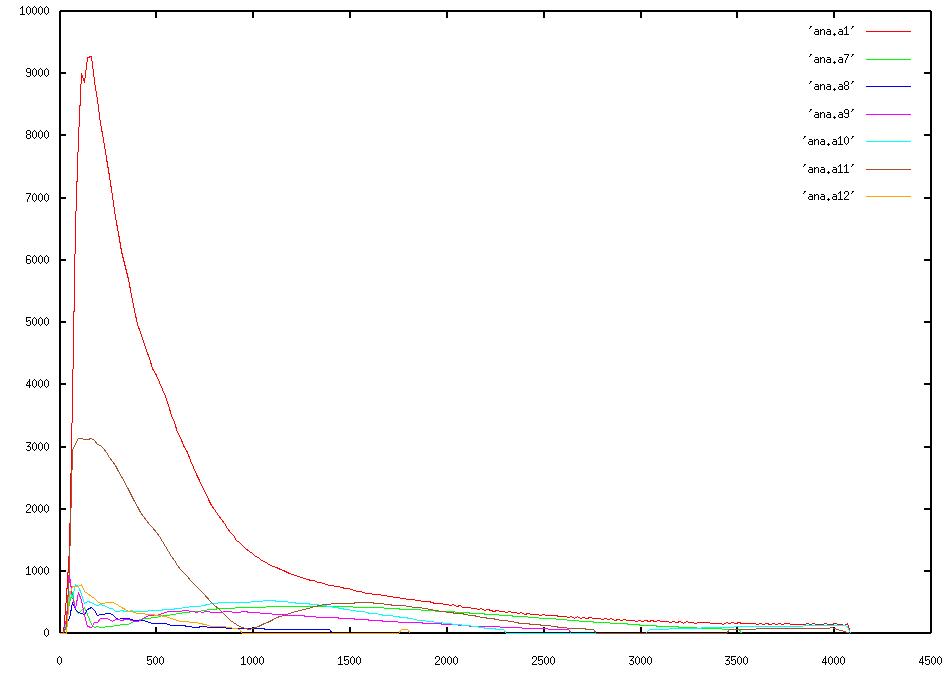
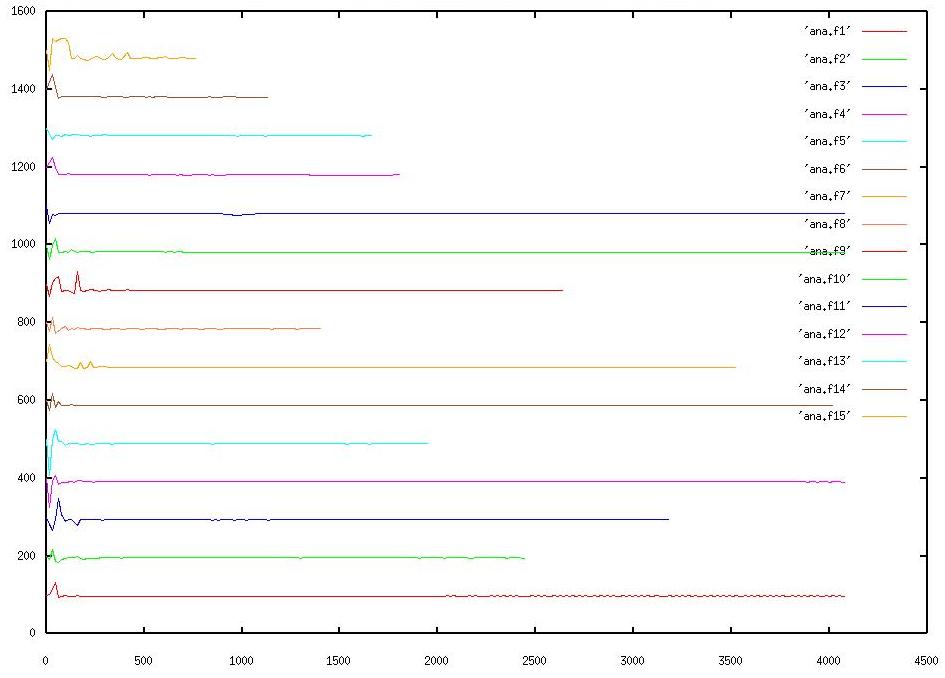
I primi 3 grafici mostrano gli inviluppi delle componenti da 1 a 24. La 1 è la fondamentale ed è riportata in tutti i grafici, per confronto.
Qui l'ampiezza è espressa in una scala assoluta da 0 a 10000, il che può far sembrare la fondamentale molto più forte delle altre componenti, ma in realtà la differenza non è così grande. Ricordate che fra 10000 e 5000 ci sono solo -6 dB, che diventano -12 a 2500 e -18 a 1250, per cui anche una componente di ampiezza 1000 è sotto di circa 18 dB e si sente bene.
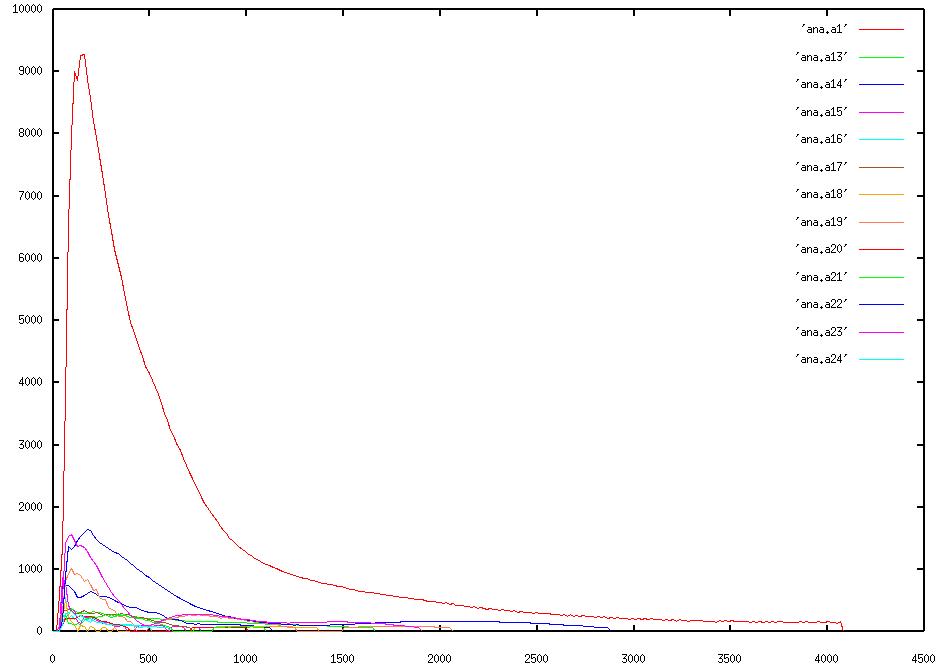
In questo grafico, invece, abbiamo gli inviluppi in frequenza delle componenti da 1 a 15. Chiaramente il pianoforte non ha vibrato, per cui le frequenze sono stabili. Si vede la difficoltà di stima della frequenza nell'istante dell'attacco in cui c'è molto rumore e il suono non è ancora stabilizzato. Il tremolio finale, invece, dipende dal fatto che il volume del suono è molto basso e la stima è anche qui difficile.
L'analisi reale prosegue per molte altre componenti. In seguito tutti i dati vengono passati al modulo di CSound 'adsyn' che effettua la sintesi. Nonostante la semplificazione nell'analisi, il risultato della simulazione è buono se il suono ha componenti armoniche o quasi armoniche. Qui sotto potete ascoltare vari esempi commentati.
Il software Ceres3 (disponibile, che io sappia, solo su linux o un qualsiasi sistema unix) utilizza la sintesi granulare sincrona in cui tutti i grani hanno la stessa durata e grani successivi sono parzialmente sovrapposti in cross-fading, con inviluppi che ne consentono la fusione.
In pratica, questo sistema è molto vicino all'analisi perché anch'essa è granulare. Per realizzare un sonogramma, infatti, vengono eseguite fino a 100 analisi per ogni secondo di suono. Il risultato, quindi, può essere visto come una serie di grani sonori (ogni analisi = 1 grano) che, posti in cross-fading l'uno dietro l'altro, ricostruiscono l'originale.
Il primo vantaggio di questo sistema è che le componenti non vengono filtrate come in hetro e così ceres3 risintetizza senza problemi anche suoni non armonici, come si può apprezzare ascoltando questo gong in originale e nella risintesi.
Il secondo vantaggio, non banale, è che, mentre hetro è legato al concetto di isolamento degli armonici e quindi obbliga a lavorare su suoni singoli, ceres permette di elaborare anche frammenti sonori formati da più di una nota e/o suoni, come testimonia questo frammento della 9a in originale (in mono, perché, come già detto, le analisi si fanno su file monofonici) e relativa risintesi.
Lo svantaggio è che, rispetto a hetro, si perde l'isolamento degli armonici. Ai programmi di elaborazione basati su hetro si può dire "togli la 3a armonica". Con ceres, invece, non si può più parlare di singole componenti, perché potendo lavorare anche su frammenti complessi come quello appena visto, il concetto di singola armonica o di singolo suono non esiste, ma bisogna lavorare sulla massa.
1.3.3 Elaborazione dei dati di analisi e successiva risintesi
Ora sentiremo alcuni esempi di modifica dei suoni mediante elaborazione
dei dati di analisi prima di procedere alla risintesi.
In questo esempio, il sol di pianoforte che abbiamo usato poco fa viene trasformato in un suono inarmonico andando a cambiare le frequenze delle componenti. Notate come anche la fondamentale sembri alterata (in effetti non c'è più una sola fondamentale). Inoltre il suo attacco viene smussato allungando leggermente i tempi.
Qui, invece, il frammento della 9a viene trasformato con ceres3, prima semplificando lo spettro eliminando tutte le componenti che non sono un picco dell'inviluppo spettrale (in pratica vengono mantenute solo le più importanti: notate come l'orchestra sembri ridotta) e poi selezionando per ogni grano solo le 5 componenti più forti e eliminando tutte le altre. Notate come la voce rimanga intelleggibile, a conferma dell'estrema specializzazione del nostro sistema percettivo.
Sempre la 9a: qui tutte le componenti sono state spostate su una griglia basata su una scala pentatonica.
Esempi basati sulla voce di Dylan Thomas che abbiamo già ascoltato
1. Sintesi basata sui dati di analisi
Dopo aver analizzato un suono su tutta la sua estensione, si possono utilizzare questi dati per effettuare una risintesi, cioè ricostruire il suono di partenza con vari procedimenti.Il primo, del tutto meccanico, è quello della FFT inversa (IFFT). Si tratta di una semplice inversione della FFT, con cui, dai dati dell'analisi, si ricostruisce l'onda che li ha generati.
Dal punto di vista musicale, però, questo sistema non è molto interessante perché non permette di apportare alcuna modifica al suono. La cosa veramente interessante, invece, è la possibilità di effettuare l'analisi, modificare i dati e infine sintetizzare un nuovo suono così elaborato.
E' chiaro che l'elaborazione effettuata sui dati ricavati dalla FFT (cioè nel dominio della frequenza) è molto più raffinata e precisa di quella effettuata sulla forma d'onda (nel dominio del tempo) con programmi come Cool-Edit e simili. Questo perché, nel dominio della frequenza si vanno a modificare dei puri numeri che possono essere cambiati anche singolarmente senza effetti collaterali. Per fare un esempio banale, in un suono basso con molti armonici l'eliminazione di una singola componente senza toccare le altre è quasi impossibile perché un filtro notch (che elimina una banda ed è l'inverso del passa-banda), per quanto stretto, ha sempre qualche effetto anche sulle componenti vicine. Lavorando sui numeri, invece, basta cancellare totalmente quella componente azzerando tutti i suoi valori di ampiezza, senza effetti sulle altre.
Molto bene. In teoria abbiamo un potente sistema di elaborazione del suono, ma dov'è il problema? Come dice uno dei corollari della Legge di Murphy, "c'è sempre un ulteriore disastro". Qui il disastro è costituito dal fatto che tutti quei numeri che noi interpretiamo come componenti, per il computer non significano nulla, ma sono soltanto numeri.
Pensate, per esempio, al sonogramma di un suono con componenti armoniche. Noi vediamo delle linee orizzontali e diciamo "ecco gli armonici", ma il computer non ha un concetto del genere. Non ci arriva nemmeno vicino. Per lui non esiste nemmeno il sonogramma nella sua interezza, ma soltanto un grafico in cui plotta, uno dopo l'altro, i risultati di centinaia di FFT. Siamo noi che, con la nostra capacità di sintesi, diamo un significato al sonogramma.
Il computer non può nemmeno capire, per es., un concetto come "la terza componente" perché lui ha in mano i dati di centinaia di FFT disgiunte in cui la terza componente non è sempre la stessa. In un suono di pianoforte, all'inizio c'è il rumore del martelletto e quindi la terza componente è una di quelle che fanno parte del rumore, mentre a metà nota è effettivamente la seconda armonica. Altro esempio: in un suono vibrato, come può il computer capire che quella frequenza che in una analisi è 2000 Hz, in quella seguente a 2050 Hz e in quella dopo 1990, in realtà sono la stessa componente?
Per lavorare in questo modo è evidentemente necessario un sistema di riduzione dei dati che, oltre a fornire al computer qualche informazione in più, lo aiuti a isolare le componenti importanti e a ricostruire un quadro complessivo coerente.
1.3.1 Simulazione mediante Sintesi Additiva classica: Hetro
Hetro è una utility che fa parte del noto programma di sintesi CSound dal quale viene lanciata con il comando 'csound -U hetro'.Questo software cerca e (possibilmente) individua le componenti armoniche di un dato suono (compresa la fondamentale) e produce, per ognuna di esse, una serie di dati che ne descrivono la variazione in frequenza e in ampiezza. Tali dati sono, poi editabili con appositi software e infine vengono passati al modulo adsyn di CSound (ADditive SYNthesis) che esegue la sintesi. Si tratta di sintesi additiva classica perché ogni sinusoide viene generata a parte con i propri inviluppi in ampiezza e in frequenza.
Hetro funziona al meglio su suoni con componenti armoniche o quasi armoniche. Ciò non toglie che possa dare buoni risultati anche con suoni inarmonici, ma solo se le componenti sono ben isolate (NON rumore). Il suo nome, infatti, deriva dal vecchio filtro a eterodina che nella versione digitale è rimpiazzato da un ben più preciso filtro COMB, la cui risposta in frequenza è costituita da una serie di picchi ugualmente distanziati in Hertz e quindi corrispondenti agli armonici di una fondamentale f1, come nella figura seguente.

Per lavorare bene, ha bisogno di alcune informazioni:
- la frequenza fondamentale in Hz. Questa
è l'informazione
principale e
deve essere molto vicina a quella del suono da analizzare. Di
conseguenza, l'utente deve già conoscere la fondamentale, cosa
d'altronde semplice perché parliamo di suoni con componenti armoniche.
Basta fare una FFT in un punto significativo.
Se la fondamentale è errata, il suono risintetizzato avrà dei 'disturbi' che dipendono dal fatto che hetro usa questo valore per piazzare le bande del filtro di cui sopra e isolare gli armonici. Se ognuna di queste bande non contiene uno e un solo armonico si avranno errori di valutazione. - la frequenza di campionamento è necessaria solo se il suono da
analizzare non è in un formato che la specifica. I formati AIFF e WAV,
specificano SR nell'header, per cui non è necessario fornirla al
programma.
- il numero di componenti da cercare. Disponendo di un computer
potente,
è bene porre questo limite molto in alto (es. 50, 100) assicurandosi,
però,
di non superare il limite SR/2. Per es., se la fondamentale è 100 Hz e
SR è 44100, il centesimo armonico di 100 è 10000, quindi è minore di
SR/2, per cui anche cercare 100 componenti è possibile (al limite
quelle più alte avranno ampiezza 0). Ma se la fondamentale è 1000 Hz,
si potrà arrivare al massimo alla componente 22 perché la 23 è 23000 e
eccede SR/2. Notare che in questo caso non si produce un errore nella
fase di analisi, bensì in fase di risintesi (cioè dopo).
- la soglia di ampiezza al di sotto della quale una componente è considerata ininfluente. Il default è -54 dB, ma disponendo di un computer potente, è bene mettere 0 (zero, cioè mai).
I primi 3 grafici mostrano gli inviluppi delle componenti da 1 a 24. La 1 è la fondamentale ed è riportata in tutti i grafici, per confronto.
Qui l'ampiezza è espressa in una scala assoluta da 0 a 10000, il che può far sembrare la fondamentale molto più forte delle altre componenti, ma in realtà la differenza non è così grande. Ricordate che fra 10000 e 5000 ci sono solo -6 dB, che diventano -12 a 2500 e -18 a 1250, per cui anche una componente di ampiezza 1000 è sotto di circa 18 dB e si sente bene.



In questo grafico, invece, abbiamo gli inviluppi in frequenza delle componenti da 1 a 15. Chiaramente il pianoforte non ha vibrato, per cui le frequenze sono stabili. Si vede la difficoltà di stima della frequenza nell'istante dell'attacco in cui c'è molto rumore e il suono non è ancora stabilizzato. Il tremolio finale, invece, dipende dal fatto che il volume del suono è molto basso e la stima è anche qui difficile.

L'analisi reale prosegue per molte altre componenti. In seguito tutti i dati vengono passati al modulo di CSound 'adsyn' che effettua la sintesi. Nonostante la semplificazione nell'analisi, il risultato della simulazione è buono se il suono ha componenti armoniche o quasi armoniche. Qui sotto potete ascoltare vari esempi commentati.
| Originale |
Simulazione |
Commento |
| piano |
piano | Manca
il rumore del martelletto perché hetro non può simulare i rumori. Come
in molti sistemi di sintesi, i rumori di questo tipo si possono
campionare e inserire a parte. |
| cello |
cello |
Qui
manca il rumore dell'arco sulle alte frequenze. |
| tromba |
tromba | Anche
qui manca un po' di rumore sulle alte frequenze.
Il suono risulta forse troppo pulito, ma è buono. |
| oboe |
oboe |
Nel
complesso il migliore, perché in questo suono il rumore ha minore
influenza. |
| parlato |
parlato |
La
voce parlata viene ricostruita correttamente (il testo si capisce), ma
notate come si senta nettamente la presenza di una pseudo-fondamentale
inesistente nell'originale. Questo perché, a causa del filtro, sono
state enfatizzate le componenti vicine al valore indicato come
fondamentale, necessario per utilizzare hetro. |
1.3.2 Simulazione mediante Sintesi Granulare sincrona: Ceres3
Un altro sistema utilizzato nella risintesi è quello della sintesi granulare. In questo modello di sintesi, il suono è formato da 'grani', cioè suoni molto brevi (generalmente da 10 a 100 msec) concatenati e/o sovrapposti fino a eliminare la sensazione di granulazione.Il software Ceres3 (disponibile, che io sappia, solo su linux o un qualsiasi sistema unix) utilizza la sintesi granulare sincrona in cui tutti i grani hanno la stessa durata e grani successivi sono parzialmente sovrapposti in cross-fading, con inviluppi che ne consentono la fusione.
In pratica, questo sistema è molto vicino all'analisi perché anch'essa è granulare. Per realizzare un sonogramma, infatti, vengono eseguite fino a 100 analisi per ogni secondo di suono. Il risultato, quindi, può essere visto come una serie di grani sonori (ogni analisi = 1 grano) che, posti in cross-fading l'uno dietro l'altro, ricostruiscono l'originale.
Il primo vantaggio di questo sistema è che le componenti non vengono filtrate come in hetro e così ceres3 risintetizza senza problemi anche suoni non armonici, come si può apprezzare ascoltando questo gong in originale e nella risintesi.
Il secondo vantaggio, non banale, è che, mentre hetro è legato al concetto di isolamento degli armonici e quindi obbliga a lavorare su suoni singoli, ceres permette di elaborare anche frammenti sonori formati da più di una nota e/o suoni, come testimonia questo frammento della 9a in originale (in mono, perché, come già detto, le analisi si fanno su file monofonici) e relativa risintesi.
Lo svantaggio è che, rispetto a hetro, si perde l'isolamento degli armonici. Ai programmi di elaborazione basati su hetro si può dire "togli la 3a armonica". Con ceres, invece, non si può più parlare di singole componenti, perché potendo lavorare anche su frammenti complessi come quello appena visto, il concetto di singola armonica o di singolo suono non esiste, ma bisogna lavorare sulla massa.
1.3.3 Elaborazione dei dati di analisi e successiva risintesi
Ora sentiremo alcuni esempi di modifica dei suoni mediante elaborazione
dei dati di analisi prima di procedere alla risintesi.In questo esempio, il sol di pianoforte che abbiamo usato poco fa viene trasformato in un suono inarmonico andando a cambiare le frequenze delle componenti. Notate come anche la fondamentale sembri alterata (in effetti non c'è più una sola fondamentale). Inoltre il suo attacco viene smussato allungando leggermente i tempi.
Qui, invece, il frammento della 9a viene trasformato con ceres3, prima semplificando lo spettro eliminando tutte le componenti che non sono un picco dell'inviluppo spettrale (in pratica vengono mantenute solo le più importanti: notate come l'orchestra sembri ridotta) e poi selezionando per ogni grano solo le 5 componenti più forti e eliminando tutte le altre. Notate come la voce rimanga intelleggibile, a conferma dell'estrema specializzazione del nostro sistema percettivo.
Sempre la 9a: qui tutte le componenti sono state spostate su una griglia basata su una scala pentatonica.
Esempi basati sulla voce di Dylan Thomas che abbiamo già ascoltato
- Ascolto. Tutte le frequenze delle componenti sono state spostate verso l'alto di 50 Hz. In tal modo anche un suono armonico diventa inarmonico.
- Ascolto. E' stato estratto
l'inviluppo di ampiezza del segnale e le frequenze delle componenti
sono state espanse verso
l'alto in modo proporzionale all'ampiezza del suono. In pratica, quando
il suono è più forte, l'intero spettro si sposta verso l'alto.
- Ascolto. Filtraggio altamente selettivo su 100 Hz e armonici.
- Spostamento totale delle componenti su una griglia di note predefinita, qui basata sul modo maggiore e qui sul minore armonico.
- Ascolto. Distorsione controllata
gradualmente calante.
- Ascolto. Elaborazione estrema in cui le componenti vengono disperse e granulate.