Questa possibilità esiste e in teoria è molto semplice: basta avere la risposta all'impulso tipica di quel luogo. A partire da quest'ultima, c'è un metodo per applicare quel riverbero a un suono qualunque. Ormai questa possibilità è offerta da molti software commerciali come Adobe Audition (già CoolEdit), Nuendo, Cubase (tramite plugin) e vari altri. Esistono anche dei software specializzati, come Altiverb per Mac, da quest'anno disponibile anche su PC.
Della risposta all'impulso e della formazione del riverbero abbiamo già parlato qui, comunque possiamo riprendere i concetti base.
Ritorniamo alla sua definizione: come dice il nome, la risposta all'impulso di un ambiente è la serie di echi che quell'ambiente genera in risposta a un singolo, brevissimo impulso (un 'toc' molto breve). In pratica, è la riverberazione ambientale.
Si tratta, quindi, di andare in quel luogo con un computer, scheda audio e amplificazione. A questo punto si emette un singolo 'toc' e contemporaneamente si registra la reazione dell'acustica ambientale.
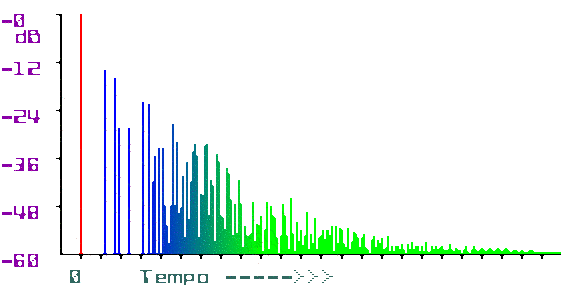 Ne esce un grafico, più o meno come quello a destra in cui
si vedono l'impulso (in rosso) e i primi echi (prime riflessioni del
suono sulle pareti, in blu), il cui addensarsi per i continui rimbalzi
sulle pareti produce, gradualmente, il riverbero (in verde).
Ne esce un grafico, più o meno come quello a destra in cui
si vedono l'impulso (in rosso) e i primi echi (prime riflessioni del
suono sulle pareti, in blu), il cui addensarsi per i continui rimbalzi
sulle pareti produce, gradualmente, il riverbero (in verde).Notate che l'ampezza (il volume) della risposta è necessariamente più basso di quello dell'impulso usato come eccitatore a causa del fatto che, anche considerando il solo spostamento nell'aria, il suono perde energia in ragione pari al quadrato della distanza percorsa.
Inoltre, come già detto nel primo articolo di questa serie, le riflessioni sulle pareti dell'ambiente assorbono molta energia. Quando incontra un ostacolo, l'onda sonora viene
- in parte riflessa,
- in parte assorbita,
- in piccola parte trasmessa al di là dell'ostacolo.
Perché filtrato sulle frequenze alte? Per due ragioni:
- quasi tutti i materiali assorbono di più le frequenze alte rispetto a quelle basse;
- l'aria assorbe un po' di frequenze alte.
| Materiale |
125
Hz |
500
Hz |
4000
Hz |
| Cemento
a vista |
0.01 |
0.02 |
0.04 |
| Mattoni
a vista |
0.02 |
0.03 |
0.06 |
| Marmo |
0.01 |
0.01 |
0.01 |
| Vetro |
0.008 |
0.008 |
0.01 |
| Legno
a vista |
0.01 |
0.04 |
0.04 |
| Linoleum |
0.02 |
0.03 |
0.05 |
| Tappeto
pesante |
0.09 |
0.21 |
0.31 |
| Tappezzeria
in velluto |
0.05 |
0.35 |
0.36 |
| Truciolato
assorbente |
0.20 |
0.64 |
0.69 |
| Pannello in fibra di vetro - max |
0.60 |
0.90 |
0.90 |
Detto in breve, tutto questo significa che se un suono a 500 Hz. e volume 100 colpisce una parete di marmo, si origina un eco a volume 99 (lo 0.01, cioè 1, viene assorbito, il resto riflesso), mentre se la parete è in velluto, l'eco ha volume 65 (lo 0.35 è assorbito, il resto riflesso). Con un materiale come il truciolato forato, il suono restituito è solo lo 0.36 dell'originale, ma oggi esistono materiali sintetici ancora più assorbenti.
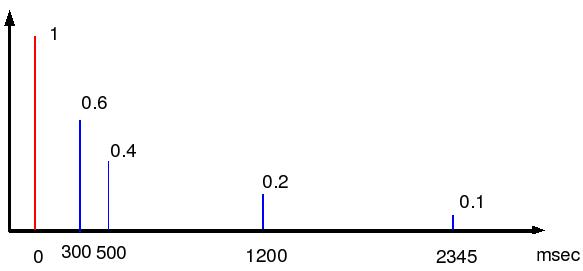
Ne consegue che l'ampiezza del 'toc' iniziale è assunta come unità di confronto per misurare il decadimento del riverbero, infatti nel grafico l'impulso è posto a 0 dB e questo permette di vedere che i primi echi sono circa 20 dB sotto l'ampiezza di partenza e così via. In tal modo il grafico è applicabile a qualsiasi ampiezza di partenza.
Metodologia di rilevamento della risposta all'impulso
Ovviamente le considerazioni che seguono valgono per il nostro fine che è quello di creare una riverberazione da utilizzare in un contesto musicale. In altre situazioni, per es. lo studio dell'acustica di una sala, si possono utilizzare metodologie diverse.La durata ideale dell'impulso è "infinitamente breve". Ovviamente si tratta di un concetto matematico. Il metodo utilizzato per la generazione dell'impulso è variabile. A volte si usa un suono reale molto breve, come un colpo di pistola, un 'ciak' cinematografico o l'esplosione di un palloncino. Esiste anche una macchina, chiamata appunto "sparkle machine", la cui funzione è di emettere suoni impulsivi.
Oggi si può anche generare un suono con un sistema digitale e inviarlo, amplificato, a uno o più altoparlanti. In un sistema digitale, la durata più breve possibile è di 1 campione. Lavorando a 44100, tale durata è 1/44100 di secondo. Naturalmente non esiste un sistema di amplificazione in grado di riprodurre una tale durata, non fosse altro per l'inerzia del cono. Comunque si approssima mandando effettivamente un impulso di un campione e usando un sistema con coni sufficientemente rigidi.
Un altro sistema è quello, più complesso, detto "sine-sweep". Si invia una sinusoide che fa un glissato logaritmico attraverso tutte le frequenze per una durata anche lunga (18 - 20 sec.). Al segnale registrato viene poi applicata una de-convoluzione che, conoscendo il segnale di partenza, è in grado di estrarre la risposta ambientale.
Il dilemma altoparlanti/oggetti, cioè il fatto di usare un impulso amplificato oppure emesso da un oggetto, non è proprio banale. Innanzitutto, l'utilizzo di un sistema di amplificazione è più complesso in termini logistici (serve la corrente, non bastano una pistola e un DAT a pile). Inoltre lo speaker deve avere una risposta per quanto possibile lineare, cosa difficile ad alto volume.
Infine, si tratta anche di capire se la risposta che si desidera deve essere generata da un suono direzionale (con la maggior parte dell'emissione concentrata in una direzione, come nel caso degli altoparlanti) o diffuso (emissione a sfera, tipo colpo di pistola). Per il nostro utilizzo si dovrebbe cercare una emissione parzialmente direzionale, cioè con buona parte dell'energia diretta in avanti e in piccola parte in alto e dietro, tipica della media degli strumenti musicali.
Un altro problema è dove piazzare i microfoni che registrano la risposta, rispetto al suono diretto. A meno di ricerche particolari, di solito si piazzano molto vicino all'oggetto che crea l'impulso. In tal modo si registra l'impulso al suo volume reale e si ottiene un rapporto corretto con il volume della risposta.
Soltanto nel caso in cui si voglia, per es., indagare su come il suono si diffonda nei vari punti della sala, i microfoni sono piazzati lontano dall'impulso.
L'ultimo punto è la scelta della posizione di microfoni e impulso nell'ambiente. Occorre cercare un punto non troppo "particolare", cioè tale da influenzare più di tanto la risposta, quindi evitare di essere molto vicino alle pareti, al pavimento, al soffitto. Nello stesso tempo, però, si dovrebbe evitare anche una posizione troppo centrale, cioè simmetrica rispetto alle pareti perché anche questa è una posizione particolare in cui le riflessioni a destra e a sinistra impiegano lo stesso tempo a ritornare. Quindi il punto ideale può essere in mezzo alla sala, ma un po' eccentrico.
Sulla metodologia sia di generazione che analisi trovate, comunque, parecchio materiale in internet facendo una ricerca come questa su Google.
Ora vediamo alcune risposte all'impulso tratte da ambienti reali.
Risposte all'impulso di ambienti reali
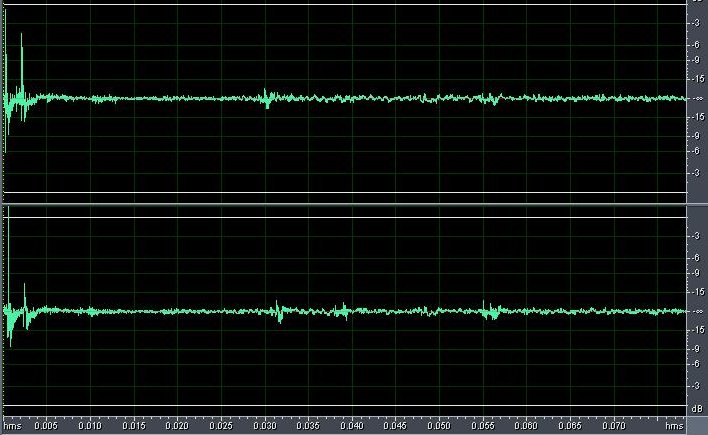
Nota: le risposte all'impulso su cui si basano tutti gli esempi sono tratte dai siti indicati oltre.In base a quanto scritto da Fokke, questa è la risposta all'impulso (IR d'ora in poi) della piccola chiesa di Schellingwoude, presso Amsterdam (canale sinistro sopra, destro sotto). Dura poco meno di 1 sec.
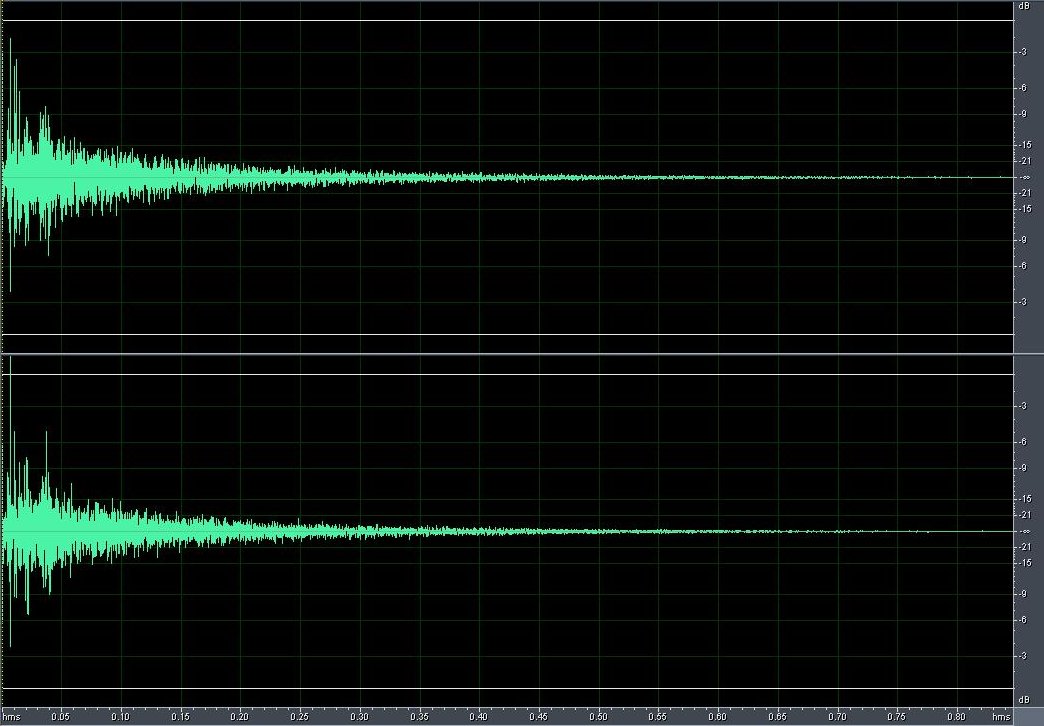
La prima cosa che si nota, rispetto al grafico utilizzato come esempio, è che gli echi sono sia positivi che negativi. Questa è la "vera realtà"; il grafico era volutamente semplificato. In base alla distanza, infatti, gli echi dell'impulso possono arrivare anche in opposizione di fase con l'effetto di colorare il segnale.
Inoltre qui abbiamo una risposta per i canale sinistro e una per il destro. Anche questo è corretto: nel mondo reale le risposte che arrivano alle orecchie sin. e des. sono necessariamente diverse. Sarebbero (quasi) uguali solo in un ambiente simmetrico (anche come disposizione degli oggetti) con sorgente e ascoltatore piazzati esattamente sulla linea mediana.
Osservate, ora, questo ingrandimento relativo ai primi 50 msec. (l'immagine è grande ma è l'unico modo di vederla bene)
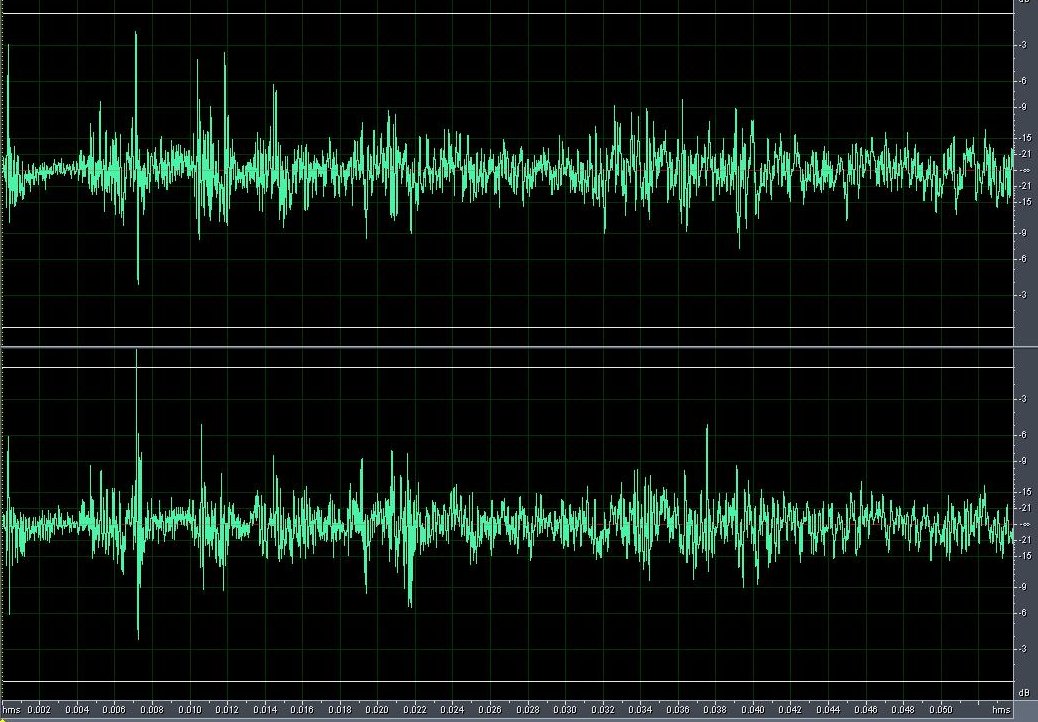
Il picco iniziale inziale, a circa 1 msec dovrebbe essere, verosimilmente, l'impulso (un colpo di pistola secondo la descrizione). Un msec corrisponde a circa 34 cm di distanza fra sorgente e microfoni.
Si nota poi un primo eco a circa 7 msec, il che corrisponde a una distanza di m 2.4. Il fatto che l'eco sia praticamente sincrono sui due canali fa pensare a una posizione centrale. Questa idea è rinforzata dal fatto che l'ampiezza del picco è perfino superiore a quella dell'impulso, da cui si potrebbe dedurre che gli echi provenienti da sin. des. siano in fase (posizione centrale = distanza uguale dalle pareti = ritorno degli echi in fase). Questo però porterebbe a concludere che la larghezza della sala è di circa 5 metri.
Questa è una immagine dell'edificio, sempre tratta dal sito di Fokke van Saane. Da qui non è possibile stimare la larghezza reale e anche altre immagini trovate su internet non ne consentono una misura sicura, tuttavia alcune suggeriscono che potrebbe essere realmente così stretta (guardate l'organo, in fondo, e pensate che le canne prendono circa 2 m).

Ora fate questo esperimento.
Ascoltate il file di cui stiamo parlando, cioè ascoltate direttamente la pura e semplice IR cliccando qui: IRChurchSchellingwoude.wav (circa 330K). Notate come, anche ascoltando la sola IR si abbia già un'idea abbastanza precisa del tipo di riverbero.
NB: i file delle IR non possono essere compressi in MP3 (cioè con una compressione lossy) perché verrebbero modificati: non si tratterebbe più della IR originale. Non sono file da ascoltare ma da usare per elaborare un altro segnale e il togliere qualcosa potrebbe tradursi in differenze di fase nelle componenti del segnale elaborato. AL massimo, si possono comprimere con una compressione loseless. Invece i file audio a cui è stata già applicata la riverberazione possono essere tranquillamente compressi.
Adesso prendiamo il suono di un rullante abbastanza secco e applichiamogli, con il metodo che vedremo poi, la riverberazione della chiesa di Schellingwoude ottenendo quello che sentite qui. Questo è il rullante come suonerebbe nella chiesa di Schellingwoude.
Per fini musicali, poi, si può mixare a questo segnale il suono diretto. È vero che, dato che la IR contiene anche l'impulso, il suono diretto c'è già, ma qui ricadiamo nell'area delle scelte estetiche. Con l'effetto di presenza dato dal rinforzo del suono diretto abbiamo questo risultato.
Come funziona
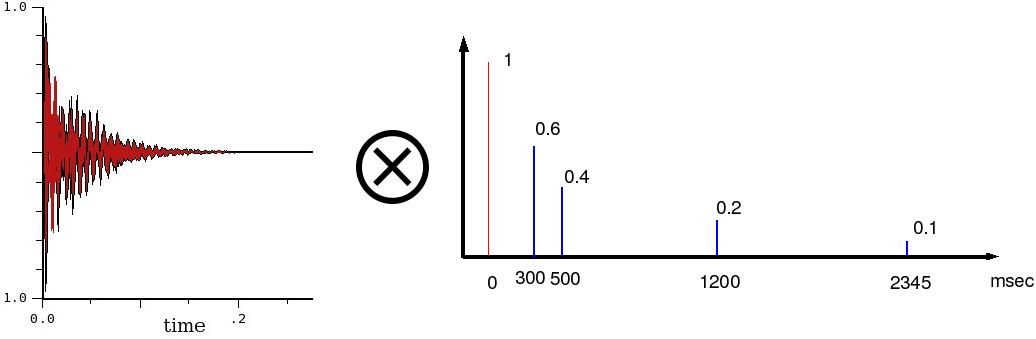
Prima di fare altri esempi, vediamo come funziona la convoluzione.In realtà è molto semplice: l'operazione di convoluzione fra due segnali consiste nel moltiplicare tutti i campioni del primo per ogni campione del secondo.
Facciamo un esempio pratico. Prendiamo il segnale del rullante usato poco fa. Come si vede si tratta di un segnale breve (circa 0.2 sec).
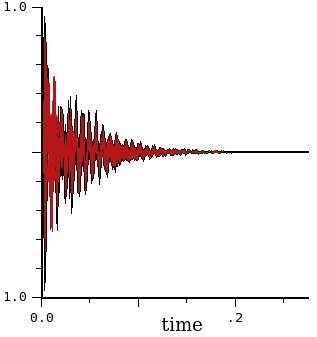
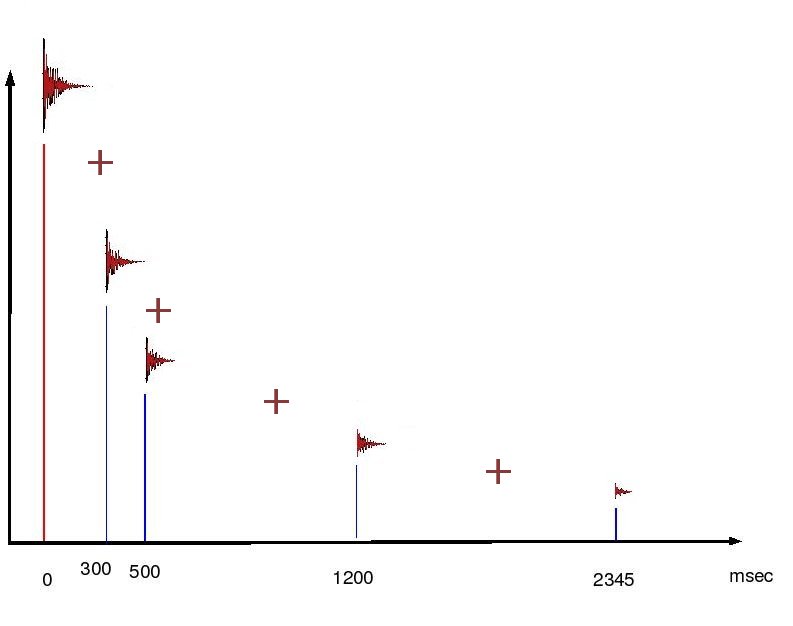
Si ottiene, così, questo che è il vero risultato finale che potete ascoltare qui
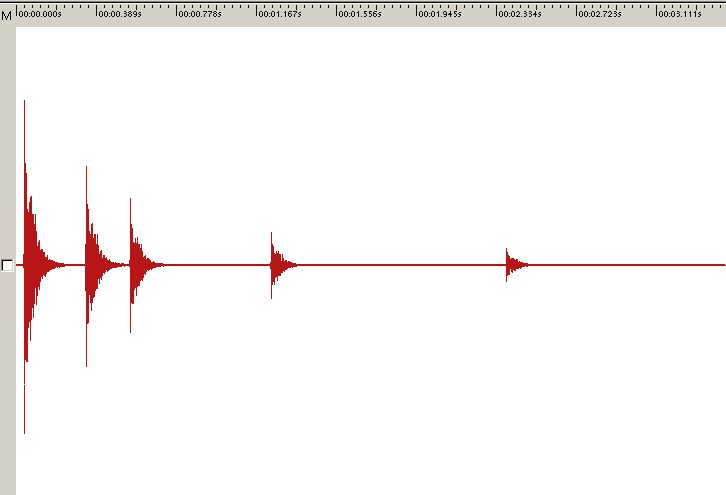
Ecco, questo è tutto. Abbiamo preso un segnale. Abbiamo calcolato la convoluzione con la IR di un determinato ambiente e ottenuto quel segnale immerso in quell'ambiente.
Naturalmente qui ce la siamo cavata con poco. In fondo avevamo un segnale breve e solo 4 echi. Anche così, però, la mole di calcoli è imponente. Se pensiamo che un segnale monofonico che dura 0.2 sec. a SR 44100 è composto da 8820 campioni, qui la macchina ha eseguito 8820 * 5 = 44100 moltiplicazioni e altrettante somme.
Per fare la convoluzione con la IR della chiesa (e in qualsiasi altro caso reale) in cui la IR è piena di echi, le moltiplicazioni e le somme da eseguire sono milioni. Ne consegue che difficilmente si può eseguire questa operazione in tempo reale. Di solito il software impiega alcuni secondi per eseguire il calcolo (alcuni software danno un preview approssimato).
Avvertenze
Ci sono alcune cose da tener presenti quando si esegue questa operazione. Il fatto che queste indicazioni debbano essere seguite o meno, dipende dal software: alcuni suppliscono senza lamentarsi, altri si lamentano, altri ancora eseguono e basta dando un risultato falsato. Comunque eccole:-
Il segnale e la IR devono avere lo stesso SR. Questa indicazione è imperativa altrimenti il risultato è falsato. Se, con SR diversi, un software non si lamenta significa che lui esegue la conversione oppure lavora alla cieca dando un risultato falso.
-
È bene che il segnale e la IR abbiano lo stesso formato: entrambi a 16 o 24 bit, ma di questo potete preoccuparvi meno perché di solito i sofware risolvono automaticamente il problema.
- Per quanto riguarda i canali, la situazione migliore si ha con un
segnale monofonico e una IR stereo. In questo caso un buon software
dovrebbe creare un segnale stereo eseguendo la convoluzione del segnale
monofonico due volte (una per ogni canale della IR) e piazzando i
risultati sui rispettivi canali.
Nel caso il software volesse lo stesso formato, basta far diventare stereo il segnale di partenza mettendolo uguale su entrambi i canali.
-
Non preoccupatevi se il risultato esce ad ampiezza bassissima: riscalatelo! Il fatto è che la moltiplicazione di due campioni numerici pone problemi di estensione. Moltiplicando due numeri interi a 16 bit si ottiene un risultato a 32 bit e due numeri a 24 bit danno 48 bit, quindi, per non bucare il range numerico, molti software fanno l'intera convoluzione con calcoli in floating point, considerando il massimo valore del campione (±32767 a 16 bit) come ±1.0.
A questo punto il risultato ha per forza di cose una ampiezza minore dell'originale perché la moltiplicazione di due numeri fra 0 e 1 dà un valore più piccolo rispetto a entrambi (es.: 0.5 * 0.3 = 0.15). Considerando, poi, che nelle IR reali ci sono molti echi in controfase, il tutto può arrivare a livelli molto bassi. - Ovviamente il segnale da riverberare dovrebbe essere il più secco
possibile. L'ideale sarebbe una registrazione in camera anecoica
(totalmente priva di echi).
Altri esempi reali
 Fabbrica
Fabbrica
Quella che vedete qui sotto è la parte iniziale della IR di un
capannone di questa
grande fabbrica (dal sito di Fokke).La risposta è stata generata con un colpo di pistola ed è caratterizzata da un singolo eco quasi immediato (circa 3 msec che corrisponde alla distanza di 1 metro: il pavimento?), seguito da una estesa coda di piccole riflessioni che creano un riverbero lungo e bello, esemplare nel suo decadimento regolare.
Potete ascoltare l'intera risposta cliccando qui.
Qui invece sentite il nostro rullante nella fabbrica.
Ho provato anche con un suono armonico che inserito nella fabbrica diventa così.
Per gli esempi che seguono sono state utilizzate alcune IR tratte dal sito di Noisevault, di cui oltre. In tutti i casi la IR è stata applicata ai seguenti suoni che potete ascoltare cliccandoli:
Chiesa del 1400
Come eccitazione è stato usato lo scoppio di un palloncino piazzato nello spazio del coro (in fondo alla chiesa, un po' elevato rispetto alla base), ma qui il microfono è stato messo in mezzo alla sala, a poco più di 10 m di distanza.Auditorium da 1800 posti
IR presa a 12 m di distanza e 4 m dal pavimento.- rullante si nota un doppio colpo
iniziale dovuto alla grandezza della sala e al fatto che l'attacco del
rullante è molto percussivo
- accordo qui infatti il colpo
doppio è quasi sparito perché l'attacco è appena più dolce
- violini qui il colpo doppio
non si sente come tale, ma il suo effetto è di addolcire gli attacchi
...altri esempi in preparazione...
Risposte all'impulso su internet
Ci sono pochi siti da cui
scaricare liberamente risposte all'impulso (potete invece
trovarne molte nei siti
dei produttori di software se siete utenti registrati, cioè avete
acquistato il software) e anche quando si trovano, spesso non sono
rigorosamente documentate, cioè non danno particolari su come e dove la
risposta è stata
rilevata. Tuttavia qualcosa si trova.Un buon posto è il sito di Fokke van Saane dai cui file sono state elaboratele alcune delle immagini seguenti. Qui si trovano parecchie risposte all'impulso interessanti, ben documentate e liberamente scaricabili. I file originali, però, sono nel formato del software Altiverb per MacIntosh: raw (senza header) big endian (byte invertiti rispetto al PC) e sono inutilizzabili su PC. Ho scritto un programma per convertirli in wav per PC che potete scaricare qui.
Il sito di Noisevault è molto interessante, ricco e documentato in modo decisamente professionale. Proprio per questo, però è più difficile per i neofiti. Le risposte all'impulso sono spesso rilevate con più microfoni in diverse posizioni rendendo meno immediato l'utilizzo dei file.
Quasi sempre è necessario leggersi i brevi testi inclusi che descrivono il microfonaggio e la corrispondenza con i file fisici. Per me è oro, ma per chi vuol fare qualcosa in fretta, non va bene.
Il materiale è già in formato wav.
Un altro sito è quello di CKSDE. Qui trovate dei file privi, però, di descrizione per cui non solo non si conoscono le condizioni di rilevamento, ma non si sa nemmeno se siano relativi a ambienti reali o generati via software. Att.ne: questi file sono sia in formato Altiverb che wav, ma a SR 48 o 96 KHz.
Tutti i siti citati contengono sia risposte di ambienti reali che ricavate da processori (ma per CSKDE non lo sappiamo).
Se ne trovate altri, per favore, fatemelo sapere segnalandoli via mail a mg AT maurograziani DOT org.