Così come la scala in semitoni, per
l'ampiezza è stata creata una scala proprio per
ovviare a questa situazione e rendere lineare ciò che in natura non lo
è. L'unità di misura è chiamata deciBel (decimi di Bel, abbr. dB). Come
quella in semitoni, infatti, la scala in deciBel è basata sui
rapporti.
In realtà, però, capire i decibel non è così semplice per varie ragioni:
- Per i decibel si utilizzano scale diverse in situazioni diverse, come vedremo
-
La percezione dell'ampiezza, poi, dipende anche
dalla distanza: se uno strumento suona a un certo volume, a voi il suono
arriverà più forte o più piano in base alla vostra distanza dallo
strumento stesso. Generalmente, in un ambiente aperto, cioè privo di
riflessioni (es: un grande spiazzo senza edifici intorno), si può dire
che, quando la distanza dalla sorgente sonora raddoppia, la pressione
sonora, cioè l'ampiezza percepita, cala di 6 dB (legge della distanza
inversa).
-
C'è una differenza fra potenza acustica e
pressione sonora (SPL cioè sound pressure level): la seconda è molto più
significativa della prima
perché rappresenta la pressione media che si esercita sul timpano ed è
quest'ultima che viene rilevata dal nostro sistema percettivo. Quando si
misura l'intensità di un segnale esterno, cioè quello emesso da
qualcosa (un altoparlante, un'auto, un aereo, etc), si misura la
pressione sonora, non la potenza acustica e in effetti si parla di
deciBelspl.
Ora, aumentare la potenza non significa aumentare nello stesso modo la
pressione sonora. Se, per esempio, avete un amplificatore da 100 Watt e
lo sostituite con uno da 200 W raddoppiate la potenza, ma non
raddoppiate la pressione sonora. Nello stesso modo, se avete di fronte a
voi un qualsiasi strumento (uno solo)
che esegue una melodia, percepite una certa ampiezza. Se adesso un altro
strumento uguale lo affianca e
suona all'unisono, si può pensare che raddoppiando la potenza, anche il
volume dovrebbe raddoppiare perché prima era uno
e adesso sono due, ma invece aumenta, ma percettivamente non
raddoppia.
In effetti, un raddoppio della potenza produce una differenza di +3 dB, mentre, per avvicinarsi a un raddoppio della pressione sonora è necessario un aumento di almeno +6 dB.
Sentiamo qualche esempio.
Qui
abbiamo un suono che diminuisce di 6 dB (quindi del doppio) a ogni
ripetizione, mentre
qui diminuisce
più gradualmente, di 3 dB.
Per avere un'idea del valore dei dB, considerate che il nostro sistema
uditivo percepisce suoni che vanno da poco più di zero (in ambiente
MOLTO silenzioso) a circa 130 dB. Quest'ultima è la cosiddetta soglia
del dolore perché un suono a questo livello è effettivamente dannoso.
Va detto, però, che il sistema uditivo è in grado di difendersi dai
suoni molto forti. Un piccolo muscolo, infatti, irrigidisce il timpano
per difenderlo dalle vibrazioni troppo ampie, mentre un altro è in
grado di mettere leggermente fuori asse la catena degli ossicini
impedendo che le vibrazioni troppo forti si trasmettano totalmente alla
chiocciola. Di conseguenza, quando ci troviamo in un ambiente ad alto
livello sonoro, sentiamo decisamente meno.
Questo sistema, comunque, ha un tempo di reazione di 1/10 di secondo e
quindi non può fare niente contro i picchi improvvisi contro i quali
siamo totalmente indifesi. Questi ultimi sono particolarmente dannosi e
possono ledere il timpano, per cui ATTENZIONE ALL'ASCOLTO IN CUFFIA che
di per sè non è affatto dannoso, ma può esporre i timpani a improvvisi
e dolorosi sbalzi se non si fa attenzione. Quando vi mettete la cuffia,
a qualsiasi strumento o impianto sia collegata, ABBASSATE PRIMA IL
VOLUME E POI ALZATELO GRADUALMENTE FINO AL LIVELLO APPROPRIATO.
Da quanto detto finora, si deduce che esistono varie modalità di misura
dell'intensità sonora di un suono, in base a quello che si vuole
misurare e alle caratteristiche del dispositivo che genera il segnale.
In ogni caso, però, la misura è sempre un rapporto fra la potenza del
segnale e un livello assunto come base. Vediamo un paio di situazioni
diverse.
Misura
L'ampiezza di un segnale si può misurare in due modi:
-
Ampiezza di picco (peak): misura il livello del picco più alto in valore assoluto (= senza considerara il segno), cioè il punto di maggiore spostamento
rispetto alla linea di zero. Questo sistema riporta l'ampiezza di un
solo punto e quindi non esprime la percezione reale del
volume di un suono, però è utile per individuare picchi che potrebbero
danneggiare il timpano o generare distorsione in un segnale elettrico.
-
Ampiezza RMS che significa root mean square cioè media
della radice quadrata della somma dei quadrati di tutti i valori. In
pratica, dato che un'onda, di solito, ha una parte positiva e una
negativa, non è possibile sommare tutti i valori e fare la media perché
numeri positivi e negativi sommati tendono ad azzerarsi. Quindi si
elevano tutti i valori al quadrato, così diventano tutti positivi, si
sommano e poi si fa la radice quadrata. Questa operazione è fatti su
piccoli segmenti di suono, lunghi da 30 a 100 millisecondi, e poi si fa
la media. Questo sistema dà un'idea più precisa del livello sonoro
percepito.
Misura dell'ampiezza di un segnale esterno (dBA, C)
La tabella qui sotto vi dà un'idea del livello sonoro di
diversi suoni (I numeri devono essere considerati come indicativi in
quanto le situazioni utilizzate come esempio non possono essere precise:
per es. non tutte le auto fanno lo
stesso rumore).
Qui si fissa come base la soglia dell'udito per una frequenza di 1000
Hz, a cui è assegnato il valore di 0 dB. Notare che questo non vuol dire
che, sotto a questo livello, non ci sia suono, ma
semplicemente che non c'è suono percepibile da un essere umano. Quando
c'è un mezzo in grado di trasmettere le onde sonore e c'è in giro
qualcosa di vivo, l'assenza di suono praticamente non esiste. Anche una
formica che cammina fa rumore. È semplicemente troppo debole per il
nostro apparato percettivo. Se si assumesse come zero l'assenza di
qualsiasi onda sonora, la soglia dell'udito si piazzerebbe fra 10 e 20
dB.
Questa modalità di misura è tipica di leggi e regolamenti che fissano
una valore massimo, tipo: una automobile non può emettere più di X dB,
oppure una band che suona in un bar non deve superare K dB, eccetera.
Tali misurazioni si fanno con un apposito apparecchio detto
fonometro
che deve essere calibrato per dare risultati precisi. La calibrazione
si effettua con un dispositivo che emette un'onda sonora a un livello
specificato in dB e su questo si regola la sensibilità dell'apparecchio.
Esistono anche app per smartphone che simulano un fonometro, ma la loro
precisione è dubbia, sia perché i microfoni non sono tutti uguali
(alcuni hanno una risposta in frequenza ottimizzata per le
caratteristiche della voce), ma soprattutto perché non vengono calibrati
se non con sistemi approssimativi.
Inoltre, quando si misura il livello sonoro, si deve tener conto anche
distanza quindi non si può dire che una automobile non deve
superare X dB senza specificare a quale distanza di deve misurare
l'ampiezza. Di solito, se nulla è specificato, la distanza si intende
pari a 1 metro.
Il fonometro, però, misura l'ampiezza puramente fisica, senza tenere
conto di alcune caratteristiche della percezione umana. Come vedremo qui
sotto (vedi "Le curve isofoniche"), il nostro sistema percettivo perde
sensibilità sui bassi e sugli acutissimi, il che significa, per esempio,
che se un violino suona una nota e un contrabbasso suona la stessa
nota, varie ottave più in basso, se si vuole che il sistema percettivo
percepisca le due note come di ampiezza uguale, il contrabbasso dovrà
suonare molto più forte del violino. Ma significa anche che, se una
macchina emette una frequenza di 1000 Hz a una ampiezza elevata, questa è
percepita come disturbante, ma, se la frequenza è a 50 Hz, non arreca
lo stesso disturbo perché il sistema percettivo è meno sensibile sui
bassi. Di conseguenza, tutte le misure vengono ponderate in
base alla frequenza per simulare la percezione umana: la misura
dell'ampiezza delle frequenze basse e acutissime viene ridotta in base
alle curve isofoniche che mappano la perdita di sensibilità del sistema
percettivo.
Esistono due tipi di ponderazione usati comunemente: A (per ampiezze
medio-basse), C (per ampiezze alte) a cui si aggiunge Z che è la misura
puramente fisica, non ponderata. Queste misure sono chiamate dBA, dBC e dBZ. In passato esistevano altri due tipi di
ponderazione: B (per ampiezze medio-alte) e D (per rumore aeroportuale), ormai obsoleti.
Nella tabella qui sotto le misure sono ponderate.
Misura dell'ampiezza di un segnale digitale o comunque di un segnale che necessita di amplificazione esterna (dBfs)
Qui le cose cambiano completamente. Nel caso di un sistema digitale, il segnale prodotto dal sistema di
sintesi è in forma numerica (uno stream di numeri) e viene inviato
alla scheda audio che lo converte in segnale elettrico tramite un
dispositivo chiamato DAC (convertitore digitale-analogico). Il segnale
elettrico in uscita dal DAC rappresenta fedelmente la forma d'onda
definita dai numeri, ma ha una potenza molto ridotta e necessita di un
amplificatore prima di essere inviato alle casse, oppure di casse
auto-amplificate, cioè con un amplificatore interno.
Per semplificare, siamo nella stessa situazione di una chitarra
elettrica, un microfono, un lettore CD. A un sistema di questo tipo non
possiamo dire "emetti un suono con ampiezza di 80 dB" ed è un grave
errore farlo, perché l'ampiezza esterna dipende dal sistema di
amplificazione.
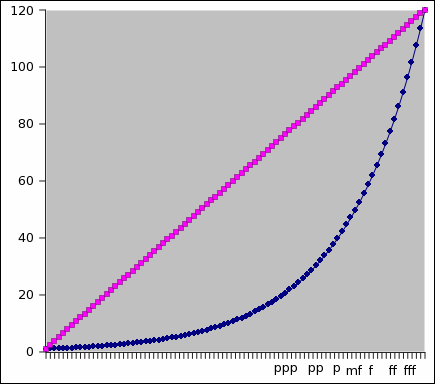
Ovviamente, usando un sistema digitale, noi possiamo generare suoni con ampiezza che va da pppp (il minimo possibile) a ffff (il più forte possibile), ma si tratta sempre di una ampiezza relativa al massimo numero accettato dal DAC e quest'ultimo dipende dal numero di bit con cui lavora.
Come sapete, attualmente esistono schede audio a 8, 16 o 24 bit. Da
questa quantità dipende la loro estensione dinamica che va, da 0 a 2(numero bit - 1) perché un bit serve a definire il segno ±. Quindi abbiamo:
- 8 bit range 0 - 127: bassa qualità, tanto che ormai viene usata solo per segnali di controllo (es. telecomandi).
- 16 bit range 0 - 32767: qualità CD
- 24 bit range 0 - 8388608: ottima qualità
NB: questo valore non influisce sulla potenza del suono che esce dalla scheda audio. Non è
detto che, a parità di amplificazione, una scheda a 24 bit suoni più
forte di una a 16 o a 8 (anzi, a volte accade il contrario). Quello che
cambia è l'estensione dinamica, cioè la differenza fra il più ppp
possibile e il più fff possibile. Considerando che ogni bit in più
raddoppia il range, cioè aggiunge 6 dB (6 db = il
doppio), per calcolarlo in deciBel basta fare numero bit * 6. Quindi
con 8 bit abbiamo un range dinamico di 48 dB (molto piccolo), con 16 di
96 dB e con 24 di 144 dB. Considerate che un'orchestra che suona un fff
supera i 100 dB a distanza ravvicinata. L'estensione dinamica del CD, quindi, non
copre quella di una grande orchestra; quella dei 24 bit, invece, sì.
Oltre a questo, il numero di bit ha anche effetti sulla qualità del suono, ma questi
li vedremo studiando il suono digitale. Ripeto: il volume che esce
dalle casse dipende principalmente dall'amplificatore, non dalla scheda
audio in sé.
Ma, alla fine, queste ampiezze come vengono espresse nei software?
Per evitare che l'utente debba dare l'ampiezza usando numeri come quelli
di cui sopra e soprattutto per fare in modo che si possa cambiare
scheda audio passando da 16 a 24 bit o viceversa senza cambiare tutti i
valori di ampiezza usati nelle patch, i software permettono di esprimere
le ampiezze in dB con un apposito formato chiamato dBfs (fs = full scale)
dove tutti i valori sono rapportati al massimo possibile, definito come zero.
Nei software, 0 rappresenta il valore massimo supportato dalla scheda
audio in
uscita, valore che non si deve superare, pena un certo livello di distorsione armonica. Tutti gli altri valori sono
negativi cioè inferiori al valore massimo. Quando un suono ha una
ampiezza di -6 dBfs significa che la sua ampiezza è 6 dB sotto al valore
massimo possibile in uscita. La conversione di questi valori in numeri
adeguati al range della scheda audio viene fatta dal software.
Ampiezze maggiori di 0 si possono sempre
usare nel corso del calcolo (sintesi o elaborazione del suono), ma il
segnale che viene inviato alla scheda audio non deve una ampiezza
superiore a 0 dBfs.
Se questo valore si supera, si ha distorsione armonica cioè creazione di
armonici che non esistono nel segnale originale (un effetto simile a
quello della saturazione della chitarra elettrica, ma meno bello;
vedremo in dettaglio cosa accade in questo caso studiando il suono
digitale).
Ampiezza assoluta (numerica)
Ovviamente è anche possibile non utilizzare i dB e misurare il suono in ampiezza
assoluta usando direttamente i numeri. Sconsigliato ai non esperti perché è come esprimere le note in Hz: bisogna lavorare
con i rapporti (la 5a di 100 Hz è 150 Hz, ma la 5a di 1000 Hz è 1500
Hz). Anche qui, comunque, i software aiutano fissando un massimo e
riscalando i valori in base al massimo della scheda audio.
Per esempio, in Max le ampiezze numeriche vanno da 0 a 1. In Csound
l'utente può scegliere il valore massimo. In entrambi i casi, il
software provvede a riscalare il massimo in base all'estensione della
scheda audio.
Conversione dBfs - Amp 0-1
Si può sempre passare da ampiezza in dBfs a numerica e viceversa. La formula di conversione da dBfs a ampiezza 0-1 è
2(dBfs/6)
Per esempio, se l'ampiezza in dBfs è -6, allora l'ampiezza 0-1 = 2
(-6/6) = 2
-1 = 0.5. Se è -3 dBfs allora = 2
(-3/6) = 2
-1/2 = 0.70710678
Quella inversa, da ampiezza 0-1 a dBfs è
6*log2(amp)
il che, usando log base 10, è uguale a
6*(log(amp)/log(2)) perché
logn(x) = log(x)/log(n)
Es: con ampiezza assoluta 0-1 = 0.5 abbiamo 6*(log(0.5)/log(2)) = 6*−0.30103/0.30103 = 6*(-1) = -6
Le curve isofoniche
Un altra cosa che complica la percezione della dinamica è il fatto che
il nostro sistema percettivo non reagisce nello stesso modo su tutte le
frequenze. Sente molto meglio nell'area che va da circa 600 a circa
5000 Hz, che è l'area del linguaggio parlato, ma soprattutto sente
molto meno sulle frequenze basse e acutissime. Questo accade perché il condotto
uditivo ha una lunghezza tale da provocare un'area di risonanza a circa
3000 Hz. Di conseguenza il livello sonoro percepito non
corrisponde all'ampiezza fisica.
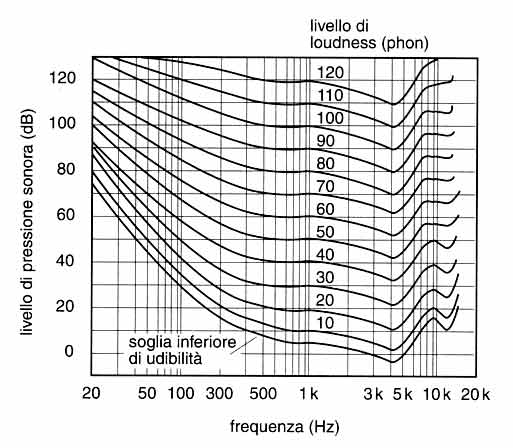
La figura seguente mostra le cosiddette curve isofoniche
(elaborate da Fletcher e Munson e note anche con il nome dei due
ricercatori) che mappano la sensazione di livello sonoro effettivamente
percepito rispetto ai dB per le varie frequenze.
Si leggono nel modo seguente: supponiamo di volere un suono a 1000 Hz
con livello sonoro percepito di 60 dB. Per sapere quale
ampiezza fisica dovremo dare a questo suono perché venga
effettivamente percepito a 60 dB
- cerchiamo sull'asse orizzontale (in basso) i 1000 Hz (indicati
con 1k; k = kilo = 1000)
- andiamo verso l'alto fino a incontrare la linea etichettata con 60
- da qui andiamo verso sinistra fino a incontrare l'asse verticale
e leggiamo l'ampiezza in dB che dobbiamo dare al segnale.
Eseguendo questo procedimento risulta che, per generare un suono a 1000
Hz con livello sonoro percepito di 60 dB, il suddetto suono dovrà avere
una ampiezza fisica di 60 dB.
Tutta questa fatica per avere un valore uguale? Sì, perché le curve
isofoniche sono tarate proprio sui 1000 Hz.
Ma adesso facciamo la stessa cosa per una frequenza a 100 Hz. Risulta
che, per generare un suono a 100 Hz con livello sonoro percepito di 60
dB, il suddetto suono dovrà avere una ampiezza fisica di circa 70 dB.
Attenzione, considerando che una differenza di 6 dB equivale al doppio,
questo vuol dire più del doppio, quasi 3 volte tanto.
La differenza, in effetti, è drammatica e aumenta andando ancora più in
basso. Se scendiamo a 50 Hz, per percepire i nostri fatidici 60 dB,
dovremo andare a circa 85 dB che significa circa 4 volte il doppio,
cioè 16 volte. Ciò significa che, per sentire avere la sensazione di
1000 Hz e 50 Hz a pari volume (60 dB), il secondo dovrà avere una
ampiezza pari a 16 volte il primo.
Ecco
una tabella che mostra la differenza dell'ampiezza percepita per suoni
a varie frequenze, rispetto a uno di 1000 Hz. Essa mostra, per esempio,
che un suono di 100 Hz che ha la stessa ampiezza fisica di uno di 1000
Hz verrà in realtà percepito come se avesse una ampiezza inferiore di
ben 19.1 dB e così via.
| 10Hz |
12,5Hz |
16Hz |
20Hz |
25Hz |
31,5Hz |
40Hz |
50Hz |
| -70,4dB |
-63,4dB |
-56,7dB |
-50,5dB |
-44,7dB |
-39,4dB |
-34,6dB |
-30,2dB |
| |
| 63Hz |
80Hz |
100Hz |
125Hz |
160Hz |
200Hz |
250Hz |
315Hz |
| -26,2dB |
-22,5dB |
-19,1dB |
-16,1dB |
-13,4dB |
-10,9dB |
-8,6dB |
-6,6dB |
| |
| 400Hz |
500Hz |
630Hz |
800Hz |
1kHz |
1,25kHz |
1,6kHz |
2kHz |
| -4,8dB |
-3,2dB |
-1,9dB |
-0,8dB |
0dB |
+0,6dB |
+1,0dB |
+1,2dB |
| |
| 2,5kHz |
3,15kHz |
4kHz |
5kHz |
6,3kHz |
8kHz |
10kHz |
12,5kHz |
| +1,3dB |
+1,2dB |
+1,0dB |
+0,5dB |
-0,1dB |
-1,1dB |
-2,5dB |
-4,3dB |
| |
| 16kHz |
20kHz |
| -6,6dB |
-9,3dB |
Facendo musica si nota che i suoni bassi si sentono un po' meno, ma non
sembra che la differenza sia così grande. Questo dipende dal fatto che
gli strumenti sono pieni di meccanismi di compensazione, sia nella
regolazione della sensibilità dei tasti del piano, che nella grandezza
delle casse acustiche.
A partire dalle curve isofoniche è stata messa a punto un'altra unità
di misura che tiene conto della frequenza e delle curve isofoniche ed è
stata chiamata Phon. Una frequenza di 100 Hz a 60
phon equivale alla stessa a 85 dB.