La catena di registrazione, quindi, è (in verde il tipo di
segnale, in rosso le apparecchiature - ADC = Analog to
Digital Converter):
Segnale audio --> Microfono
--> Segnale
elettrico --> ADC--> Segnale digitale
3.2 Riproduzione
Nella riproduzione, il
processo è inverso. Esiste un piccolo dispositivo
chiamato questa volta DAC (Digital to Analog Converter =
convertitore digitale - analogico), presente nelle
schede audio e in apparecchi come i lettori di CD, che
converte il segnale dalla forma numerica (digitale) a
corrente elettrica.
La catena di riproduzione, quindi, è
Segnale digitale --> DAC -->
Segnale elettrico --> Amplificatore --> Altoparlanti
-->
Segnale audio
4. Caratteristiche della codifica
PCM
4.1
Frequenza di campionamento
Si presenta ora il
problema di definire una frequenza di campionamento,
cioè di stabilire quanti campioni prendere per ogni
secondo di suono. E' intuibile che, maggiore è il numero
di campioni, meglio sarà definita la forma d'onda, fino
ad arrivare al punto in cui il segnale digitale è
indistinguibile dall'originale.
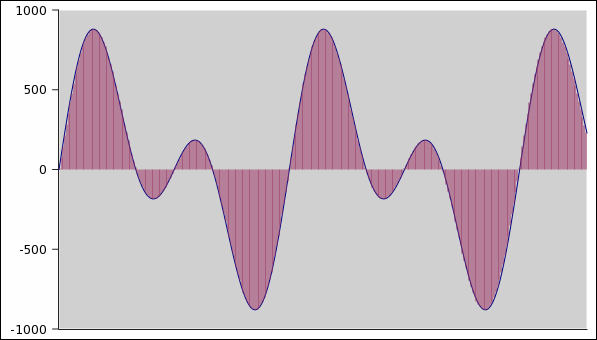
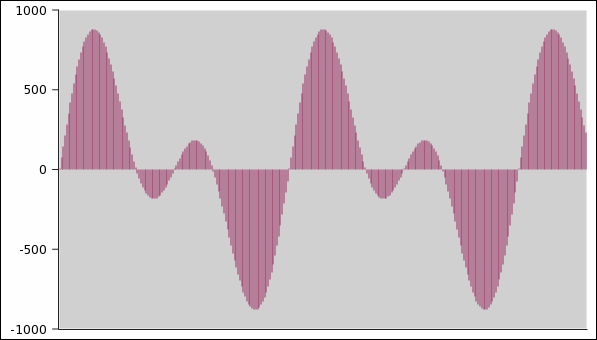
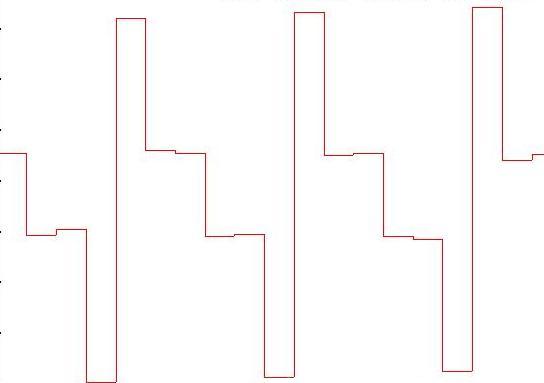
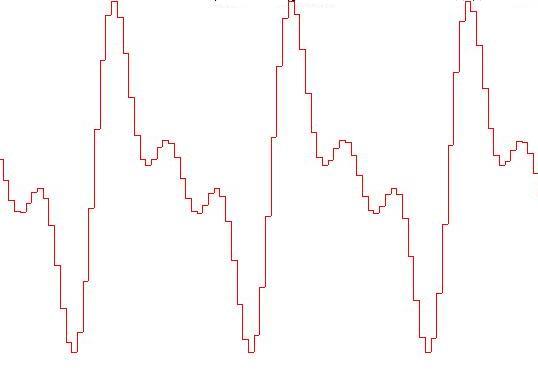
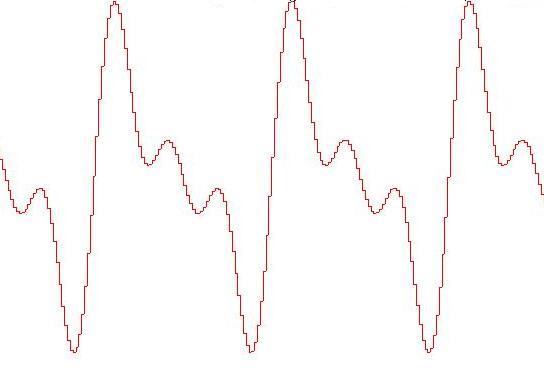
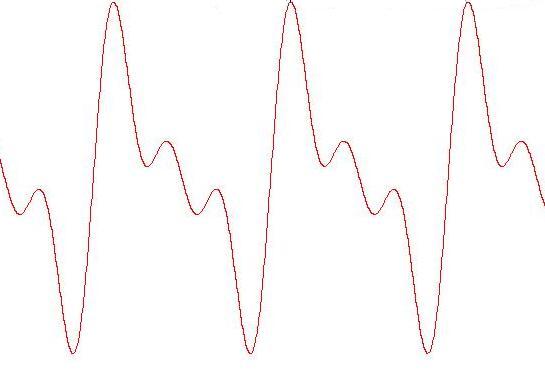
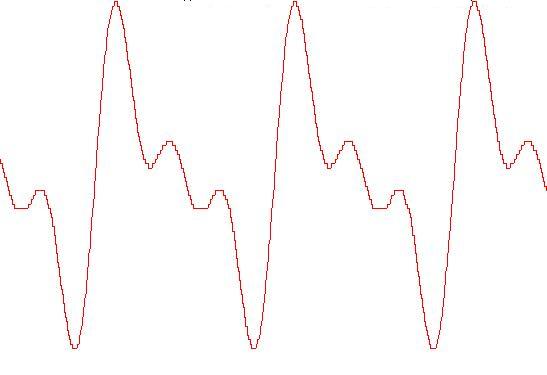
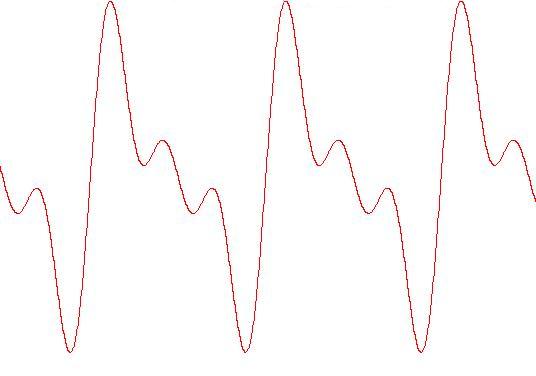
Le figure seguenti mostrano come l'approssimazione
dell'onda migliora al crescere della frequenza di
campionamento:
In generale, si può
affermare che il principale effetto di una frequenza di
campionamento (detta anche SR: sampling rate) non
adeguata è:
- perdita di frequenze alte
Negli esempi seguenti è
possibile ascoltare un frammento della 9a registrato a
frequenza di campionamento
ottimale,
metà
dell'ottimale,
bassa (qualità telefono),
bassissima:
le differenze sono evidenti (ATTENZIONE: non tutte le
schede audio consentono di riprodurre brani a frequenze
di campionamento non standard; è possibile che il vostro
computer non vi consenta di acoltare tutti gli esempi;
non si tratta di un problema).
Affrontando il problema in termini più rigorosi, esiste
un teorema (il teorema di Nyquist o del campionamento)
che dimostra come, per approssimare al meglio un segnale
audio,
la frequenza di campionamento
deve essere almeno pari al doppio della più alta
frequenza contenuta nel segnale audio
(considerando, ovviamente, anche gli armonici).
Ciò significa che con SR =
10.000, le frequenze campionabili vanno da 0 a 5000 Hz;
con SR = 20.000, da 0 a 10.000 Hz e così via. Di solito,
per indicare tale estensione. si ricorre alla nozione di
banda
passante: si dice che, con SR = 20.000, si
ottiene una banda passante da 0 a 10.000, etc.
Di conseguenza, dato che l'orecchio umano ha una banda
passante di circa 20.000 Hertz, la frequenza di
campionamento ottimale per riprodurre l'intera
estensione audio umana deve essere maggiore di 40.000
Hertz, ovvero più di 40.000 campioni al secondo. In
effetti, lo standard CD audio è stato fissato alla
frequenza di 44.100 Hertz: ogni canale di un cd, quindi,
contiene 44.100 campioni al secondo. Essendo il cd
stereo, i campioni sono 88.200 per secondo.
Altri media, che non hanno bisogno della massima
qualità, possono usare SR diversi. Per esempio, il
telefono, il cui fine è trasmettere bene la voce, che ha
una banda più limitata, utilizza una frequenza di 8.000
Hertz in mono e ha 4.000 Herz come massima frequenza
passante. Per questa ragione la musica non si ascolta
bene via telefono.
4.2
Estensione numerica (scala)
Dopo aver visto come
stanno le cose in orizzontale, vediamo la parte
verticale. All'ADC arriva un segnale elettrico di
estensione limitata (generalmente ± 5 Volt). Il
problema è: con quale grado di precisione dobbiamo
misurare questo intervallo?
Una limitazione è costituita dal fatto che, per
esigenze costruttive di ADC e DAC, nella misurazione
possiamo usare solo numeri interi: i
risultati come 2,75 non sono ammessi e vengono
approssimati all'intero (in questo caso, 2 perché
l'ADC non è in grado di arrotondare, ma tronca).
Di conseguenza, usando una unità di misura troppo
grande, pari, per esempio al Volt, con 10 passi, da -5
a +5, avremmo degli errori sensibili.
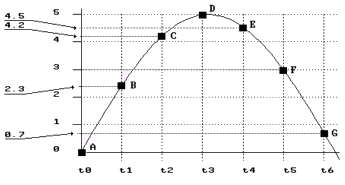
Osservate la figura a sinistra.
Il primo campione (A) vale 0 e qui va tutto bene.
Il secondo (B) vale 2,3 approssimato a 2, con un
errore di 0,3 pari al 3% sull'intera estensione
Il terzo (C) vale 4,2 approssimato a 4, errore di 0,2
pari al 2%
Il quarto (D) vale 5, errore 0
il quinto (E) vale 4,5 approssimato a 4, errore di 0,5
pari al 5%
(F) vale 3, errore 0
(G) vale 0,7 approssimato a 0, errore di 0,7 pari al
7%
In definitiva, in questo piccolo segmento di onda,
abbiamo un errore medio del 2,42%. Questi errori sono
troppo grandi per ottenere un campionamento accurato.
L'approssimazione deve essere ridotta a un valore
molto vicino a zero.
In realtà, se ci pensate, è facile eliminare i
decimali: basta usare una unità di misura più piccola.
Esempio: se misurando un oggetto si ottiene un valore
decimale come metri 2,75, per ottenere un numero
intero basta misurare in cm ottenendo cm 275. Se poi,
ci fosse bisogno di una precisione maggiore,
basterebbe passare al mm (mm 2750). Analogamente,
potremmo misurare il segnale in centesimi o millesimi
di Volt (milliVolt), eliminando quasi del tutto
l'approssimazione.
Le figure seguenti mostrano come l'approssimazione
dell'onda migliora autilizzando una unità di misura
via via più piccola
In realtà è più facile chiedersi: qual'è l'estensione
dinamica che dobbiamo coprire? In pratica, qual'è la
differenza fra il più alto volume ascoltabile senza
danni e il più basso volume percepibile?
Chi ha studiato un po' di acustica sa che l'estensione
dinamica dell'orecchio va da circa 20 a circa 120 dB
(soglia del dolore) e che ci sono grosse differenze in
base alle frequenze. L'estensione musicale è
chiaramente inferiore. In realtà un fff orchestrale
non arriva a 120 ma può essere stimato intorno ai 100
dB.
Si è convenuto, quindi, di suddividere l'estensione
dinamica in circa 60.000 passi. Il numero esatto è
65.536 pari a un numero codificato in 16 bit che
corrisponde a una dinamica di 96 dB. Ogni bit in più,
infatti, corrisponde a 6 dB di incremento dinamico.
Con 4 bit abbiamo un range di 6x4 = 24 dB; con 8 bit,
48 dB e con 16 bit arriviamo a 96. In tal modo
l'approssimazione è ridotta allo 0.0015%.
Infine, dato che le onde audio hanno una parte
positiva e una negativa, i 65.536 livelli vengono
visti come un intervallo di ± 32.768. Lo
standard
CD, dunque, è definito come
SR
44100 - 16 bit
Usare qualche bit in più (17, 18) non ha molto senso
perché il computer gestisce gruppi di 8 bit (1 byte)
come unità minima e quindi tanto vale passare a 16+8 =
24 bit con range dinamico di 144 dB (proposta DVD
audio).
4.3 Foldover
Come abbiamo detto nel capitolo 4.1, la frequenza di campionamento deve essere almeno pari al doppio della più alta frequenza contenuta nel segnale audio perché per coprire il range udibile umano che va da 0 a 20000 Hz è necessaria una frequenza di campionamento (SR) pari almeno a 40000 campioni al secondo.
Ne consegue che, in un segnale digitale, le frequenze superiori a SR/2 non esistono. Infatti, se, con quache tecnica di sintesi, create una frequenza maggiore di SR/2, la vostra frequenza non scomparirà, ma "rimbalzerà indietro" e la risultante sarà SR meno la vostra frequenza. Per es. se SR=44100, quindi con banda passante 0-22050 Hz e voi fate 30000, vi troverete una frequenza non prevista a 44100-30000 = 14100 Hz.
La stessa cosa vale per le frequenze che superano SR, per es. se fate 50000 Hz, risulta sempre 44100-50000 = -5900 e la frequenza negativa si percepisce esattamente come quella positiva con la differenza che ha la fase invertita che noi non percepiamo.
Questo fenomeno è chiamato foldover
Ne consegue che, se, per esempio, creiamo un'onda che ha più di 20 componenti armoniche, dobbiamo tener presente che, se la usiamo con fondamentale a 1000 Hz, la 20ma componente sarà a 20000 Hz che, con un SR standard di 44100 o 48000 Hz, sarà già molto vicina al limite, quindi
- eventuali componenti superiori, ma inferiori a SR/2, saranno percepibili solo dal vostro cane o gatto,
- in base alla frequenza di campionamento queste frequenze potrebbero andare in foldover producendo frequenze percepibili ma non previste.
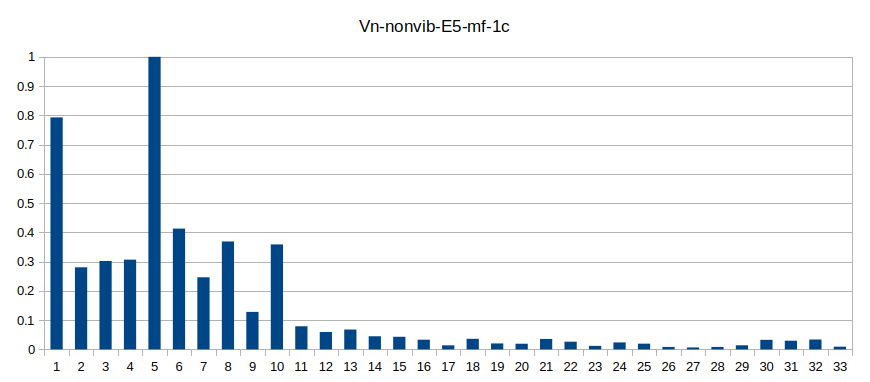
Ma questo vale per una fondamentale a 1000 Hz e una ventina di componenti armoniche. In realtà un Mi di violino a corda vuota, con fondamentale a circa 660 Hz arriva a 33 componenti.
Un esempio dello schema del suo spettro, ricavato da un suono reale, è questo:
Qui l'asse Y è in ampiezza 0-1 e i numeri sull'asse X sono quelli delle componenti: 1 è la fondamentale, 2 il primo armonico, etc. quindi questo non è uno spettro, ma lo schema dello spettro di un suono con componenti armoniche. Una volta scelta la fondamentale possiamo ottenere lo spettro con asse X in Hz moltiplicando questa frequenza per 1, 2, 3, etc.
Ora, con fondamentale a 660 Hz, la frequenza della 33ma componente è 660 * 33 = 21780 Hz, cioè appena sotto la massima frequenza oltre alla quale scatta il foldover con SR=44100. Già una ipotetica componente 34 fa 22440 Hz ed è in foldover quindi produrrebbe 44100-22440 = 21660 Hz. Una frequenza che noi non possiamo sentire, ma tutto questo significa che, con questa configurazione spettrale, in teoria non possiamo andare oltre il Mi 660 senza produrre componenti non volute con frequenze che non c'entrano nulla con questo spettro!
Adesso immagino già che qualcuno mi dirà: "ma dai, sono tutte frequenze altissime e poi nello schema hanno ampiezze ridicole…" e in questo caso avrebbe anche ragione. Ci sono casi in cui il foldover c'è ma non si percepisce. Questo può accadere quando:
- le componenti che vanno in foldover hanno una ampiezza troppo bassa per essere percepite. Considerate che una ampiezza di 0.005 è quasi -46 dBfs e 0.001 è quasi -60 dBfs. In quest'ultimo caso è ben difficile sentirle.
- le componenti che derivano dal foldover spesso hanno una frequenza così alta (> 5000 Hz) da essere attenuate anche in base alle curve isofoniche di Fletcher-Munson. L'attenuazione aumenta via via che la frequenza sale (vedi Corso di acustica - dinamica)
- a volte sono mascherate da una frequenza non lontana e di ampiezza molto superiore (vedi sempre Corso di acustica - dinamica).
- la percezione e la valutazione di componenti che non fanno parte del segnale, ma sono generate dai limiti del sistema è influenzata anche dall'affollamento dello spazio acustico in cui le componenti generate dal foldover ricadono. È chiaro che se, intorno a una componente in foldover ci sono molti altri suoni, la sua percezione potrebbe essere più difficile, ma se questi altri suoni hanno una organizzazione leggibile (e.g. tonale o armonica), l'intrusione di una frequenza estranea sarà immediatamente riconoscibile.
- N.B. tutte queste considerazioni valgono se i test di ascolto vengono fatti con un buon impianto/cuffia.
 Ma calma, vediamo un esempio. Il Do più alto del piano che, a parte qualche caso sporadico, possiamo considerare come la fondamentale più alta nella nostra musica, è 4186 Hz. Se semplicemente andiamo al La della penultima 8va del piano che è 1760 Hz, il nostro spettro va in foldover già alla 13ma componente. Andando su di un'altra 8va siamo a 3520 che va in foldover alla 7ma componente e produce questo mentre dovremmo sentire questo.
Ma calma, vediamo un esempio. Il Do più alto del piano che, a parte qualche caso sporadico, possiamo considerare come la fondamentale più alta nella nostra musica, è 4186 Hz. Se semplicemente andiamo al La della penultima 8va del piano che è 1760 Hz, il nostro spettro va in foldover già alla 13ma componente. Andando su di un'altra 8va siamo a 3520 che va in foldover alla 7ma componente e produce questo mentre dovremmo sentire questo.
Allora guardiamo il sonogramma qui a sinistra. La nostra fondamentale è 3520 Hz quindi non dovremmo vedere niente sotto questa frequenza, mentre qui vediamo una riga doppia poco sotto i 2k e un'altra vicina allo zero. Inoltre dovremmo vedere un armonico ogni 3520 Hz, quindi a circa 7k, 10k, 14k, 17k, etc. mentre vediamo molte righe in più, fra 5 e 6k, vicino a 9k, fra 12 e 13k, etc.
Cosa sono? Foldover ovviamente, infatti guardiamo quelli righe sotto i 3520. La 13ma componente del nostro segnale sarebbe 45760 Hz che va in foldover e diventa 1660 Hz, la 12ma è 42240 e diventa 1860 Hz. Ecco spiegata la doppia riga poco sotto i 2k.
E la riga molto vicina allo zero, da dove viene? Con un po' di pazienza si trova: la 27ma componente sarebbe 95040 Hz, che diventa 43650 Hz che, sottratto ancora a 44100 dà 450 Hz. Nonostante nello spettro sia molto debole (≈0.00423 cioè -47 dBfs) forse non si sente, ma si vede.
Andando avanti così, con pazienza, si può identificare tutto.
Poi ascoltate quest'altro esempio in cui abbiamo due suoni: il primo a 3520 Hz e il secondo a 1760 che sarebbe una 8va sotto, ma invece sembra quasi che sia più acuto.
Ma allora, com'è la realtà? Nella realtà non c'è il foldover quindi, se io, con uno strumento musicale, faccio l'ultimo Do del piano che è 4186 Hz, il 10mo armonico è 41860 Hz, il 20mo è 83720 e il 30mo sarebbe addirittura 125580 Hz. Ci sono veramente armonici a queste frequenze? E se ci sono, cosa succede se tento di registrarli?
La risposta alla seconda domanda è semplice: non puoi. Quando registriamo in digitale noi selezioniamo una frequenza di campionamento e tutto ciò che è maggiore di SR/2 in registrazione di solito viene brutalmente eliminato dalla scheda audio prima di arrivare all'ADC. Non si registra, punto. Da questo deriva anche il fatto che, se analizziamo suoni sempre più acuti, ci sembra che le componenti alte gradualmente spariscano, ma nella realtà non è così. Sicuramente diminuiscono in ampiezza, ma, a volte, non spariscono del tutto. Semplicemente superano le nostre capacità percettive e anche quelle della scheda audio. È per questo che non è una buona idea portare il cane a un concerto di musica classica o comunque con un'orchestra che suona dal vivo senza amplificazione (se invece gli strumenti sono amplificati, ci pensano i microfoni e le casse a far fuori tutto ciò che supera i 22 o 25 kHz, ma spesso c'è un volume tale che il cane si incazza lo stesso).
Per quanto riguarda la prima domanda, cioè la realtà, c'è un famoso paper scritto negli anni '90 da tale James Boyk del Caltech che, equipaggiato con una scheda audio e un microfono in grado di catturare il suono con una larghezza di banda che arriva a 100 kHz, ha analizzato dei suoni strumentali dimostrando che "There's life above 20000 Hertz!". Questo è il titolo dell'articolo di cui potete leggere una mia breve recensione che riporta anche il link all'articolo originale (si apre in un nuovo tab del vostro browser).
In pratica, la ricerca di Boyk dimostra, ad esempio, che una tromba che suona un Sib con fondamentale a soli 465.4 Hz emette componenti armoniche che superano i 50 kHz, arrivando anche al centesimo armonico con un'ampiezza sì bassa, ma non proprio banale.
Adesso potreste anche chiedervi se c'è un modo per evitare il foldover? Beh, evitarlo, no, ma renderlo inoffensivo sì. Basta aumentare la frequenza di campionamento. Ormai tutte le schede audio, ma anche la schedina che c'è dentro il computer, non sono limitate a 48 kHz, ma arrivano a 96 e 192 kHz.
Quindi se, per esempio, l'SR è 96000, la banda arriva a 48000. Ne consegue che:
- le frequenze ≤ 48000 Hz non vanno in foldover;
- anche una parte di quelle che vanno in foldover non si sentono se in origine sono ≤ (96000-20000) = 76000, quindi, se create una frequenza compresa fra 48000 e 76000 Hz, va in foldover ma produce una frequenza > 20000 Hz, quindi non è percepibile e in genere, viene anche annullata dalle casse;
- se poi si va a SR = 192 kHz queste misure diventano: fino a 96 kHz senza foldover e e fino a 172 kHz con foldover non percepibile.
infatti, con SR = 192 kHz, possiamo tranquillamente sintetizzare l'esempio precedente e avere un suono pulito. Un po' di foldover c'è perché ci sono delle componenti > di 96 kHz, ma non è percepibile. Lo vedete nell'immagine qui sotto, nella prima nota a 3520 Hz in cui le componenti raddoppiano da circa 75 kHz in su. In effetti qui la componente 33 è 116160 Hz che, in foldover, diventa 75840 Hz quindi questa e tutte le altre componenti > 76 kHz rimbalzano indietro. Ecco perché nel sonogramma vedete molte componenti in più a partire da circa 76 kHz.
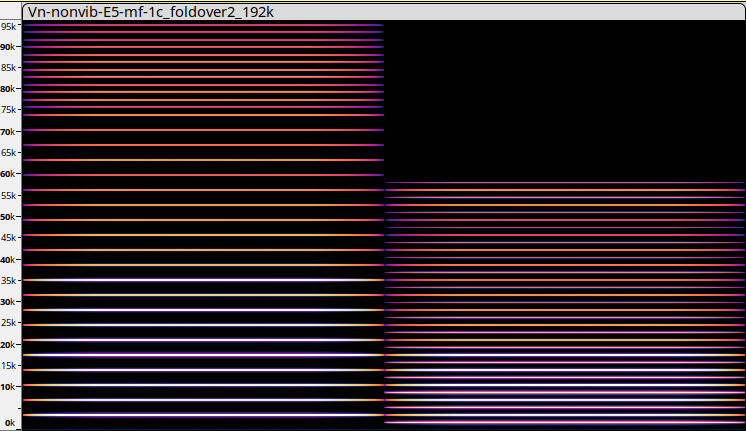
Al limite, se proprio dovete usare un SR più standard, si può sintetizzare il segnale a 192 kHz, come ho fatto qui e poi filtrare tutto sopra i 24 kHz e ricampionare con SR 48 kHz. Attenzione: non ricalcolare, ma semplicemente rileggerlo con SR 48 kHz. Ecco il risultato audio e il sonogramma. Naturalmente qui ci sono molte componenti in meno perché sono state eliminate tutte quelle > 24 kHz, che comunque non erano percepibili quindi il risultato acustico non è cambiato. Una volta fatto questo, l'audio è stato ricampionato con SR 48000.
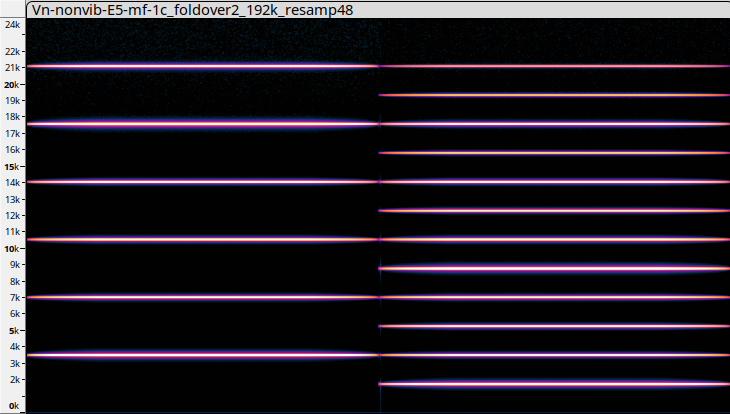
In definitiva, con SR = 96 kHz, potete tranquillamente generare frequenze < 76000 Hz senza problemi se non il fatto che il sistema lavora il doppio e questo, in tempo reale, dimezza le vostre possibilità di elaborazione e di polifonia. Con SR = 192 kHz arrivate a 172 kHz ma la performance del computer si riduce fino a circa 1/4. Allora, se, per esempio, con Max o PD, io voglio seguire in tempo reale l'inviluppo di uno strumento esterno per poterlo mixare con un mio suono dando anche a questo lo stesso inviluppo, vado a leggere l'ampiezza del segnale esterno ogni, diciamo, 5 o 10 msec e magari devo farlo per i singoli strumenti di un quartetto d'archi o di un quintetto di fiati, ce la faccio?
In effetti, questo sistema evita il foldover, ma fa lavorare il computer molto di più producendo una quantità di componenti che non servono a niente perché non sono percepibili e come già detto, questo significa ridurre le risorse a disposizione.
Conclusione: il foldover è da evitare, a meno che non sia previsto e parte del progetto oppure sicuramente non percepibile.
4.4.1
Definizioni
Distorsione
Modifica di un
segnale audio dovuta alla modifica della sua forma
d'onda, con conseguente variazione delle componenti
presenti nel segnale originale. Esistono vari tipi di
distorsione e come vedrete in questo e altri corsi,
essa non è sempre un male: in genere, è un male quando
non è voluta, ma in certe situazioni, può essere
creata e controllata.
Distorsione armonica:
introduzione di componenti armoniche non presenti nel segnale
originale. È un male quando il fine è campionare o
riprodurre un segnale audio con la maggiore fedeltà
possibile (come nel caso di cui abbiamo appena
parlato). Non è un male e viene creata appositamente
quando il fine è cambiare le caratteristiche di un
suono (elaborazione) o arricchire una sonorità (es.
tipico: i distorsori per chitarra elettrica) o ancora,
nella sintesi del suono per creare armonici partendo
da una sinusoide (es.: sintesi con tecniche di
distorsione non lineare).
Distorsione spettrale:
alterazione delle ampiezze delle componenti di un
suono: non si aggiungono componenti, ma si cambia
l'ampiezza di quelle presenti. In pratica, si
rimodella lo spettro del suono.
Distorsione per
intermodulazione: dovuta all'introduzione di
nuove frequenze generate dalla somma e/o differenza
tra frequenze componenti il segnale originario.
Rumore
Interferenza con il
suono originario che può essere sia di natura
elettrica che acustica.
Nella teoria dell'informazione, qualsiasi
segnale che interferisca con quello che ci interessa è
detto rumore (es.: se in una festa stiamo cercando di
capire quello che dice una certa persona, le altre
voci sono rumore).
Rumore di
quantizzazione (anche Errore di quantizzazione):
distorsione causata dal fatto che l'operazione di
quantizzazione introduce un'approssimazione sul
voltaggio da convertire in campione durante la
conversione di un segnale da analogico a digitale
4.4.2
Utilità
Dopo aver visto le
principali caratteristiche di un segnale audio in forma
digitale, è utile imparare a calcolare rapidamente
alcune cose.
Dimensioni
di un file audio
Ci riferiamo alle dimensioni che un file audio assume
quando viene scritto su disco o caricato in memoria. In
altre parole, allo spazio che occupa. Nel computer, lo
spazio è misurato in bytes (8 bit).
Le dimensioni di un file audio dipendono da 4 parametri:
- la durata del suono
- il numero dei canali
- la frequenza di campionamento SR
- la codifica dei campioni (8/16/24 bit = 1/2/3 bytes
ciascuno)
Per cominciare e avere
una unità di misura, calcoliamo le dimensioni di un
segnale con le seguenti caratteristiche:
durata = 1 sec;
canali = 1 (monofonico)
SR = 44100
codifica 16 bit = 2 bytes.
Ora, è semplice capire che, se ogni campione occupa 2
bytes e per ogni secondo abbiamo 44100 campioni, la
dimensione totale è di 44100 x 2 = 88200 bytes. Un
secondo di suono in monofonia, SR 44100 a 16 bit
occupa 88200 bytes.
Lo standard CD audio, comporta 2 canali (stereo; non è
possibile mettere su un normale CD dell'audio
monofonico). Con un suono stereo (2 canali), avremo sia
i campioni del canale destro che quelli del canale
sinistro, separatamente. Di conseguenza, dovremo
moltiplicare ulteriormente per 2. 88200 x 2 = 176400
bytes, quindi un secondo di suono in stereofonia in
qualità CD occupa 176400 bytes.
Ne consegue che un minuto di suono in qualità CD occupa
176400 x 60 = 10.584.000 bytes.
A questo punto è molto facile calcolare le dimensioni di
suoni di qualsiasi durata in qualità CD. È anche
possibile trovare una formula generale valida per
qualsiasi qualità audio:
Dimensioni in bytes = durata in sec *
numero canali * SR * codifica in bytes
Calcolo
numero campioni per ciclo dell'onda
Nel caso di un segnale periodico, è utile saper
calcolare rapidamente quanto campioni sono contenuti in
un singolo ciclo dell'onda. Questo valore si ottiene
facilmente dividendo SR per la frequenza del segnale e
togliendo i decimali. Es.:
freq = 100 Hz, SR = 44100, allora ogni ciclo conterrà
44100/100 = 441 campioni
freq = 1000 Hz, SR = 44100, allora ogni ciclo conterrà
44100/1000 = 44.1 campioni
Calcolo
frequenza
a partire dal numero campioni
Sempre nel caso di un segnale periodico, è altrettanto
utile il calcolo inverso, ovvero conoscendo il numero di
campioni contenuti in un ciclo dell'onda e SR, trovare
la frequenza del segnale. Questo calcolo si esegue, per
es., quando in un segnale si prende un ciclo da mettere
in loop.
Anche qui il calcolo è semplice: basta dividere SR per
il numero di campioni. Es.:
numero campioni = 441, SR = 44100, allora la frequenza
sarà 44100/441 = 100 Hz;
numero campioni = 44, SR = 44100, allora la frequenza
sarà 44100/44 = 1002.27 Hz
Corrispondenza
nota
- frequenza
Qui il calcolo è più complesso (vedi CDROM Acustica). Vi
riporto questa tabella, dove trovate le frequenze
corrispondenti alle note del sistema temperato
(evidenziata l'estensione del pianoforte).
|
-1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
C
|
16.35
|
32.70
|
65.41
|
130.81
|
261.63
|
523.25
|
1046.50
|
2093.00
|
4186.01
|
8372.02
|
|
C#/Db
|
17.32
|
34.65
|
69.30
|
138.59
|
277.18
|
554.37
|
1108.73
|
2217.46
|
4434.92
|
8869.84
|
|
D
|
18.35
|
36.71
|
73.42
|
146.83
|
293.66
|
587.33
|
1174.66
|
2349.32
|
4698.64
|
9397.27
|
|
D#/Eb
|
19.45
|
38.89
|
77.78
|
155.56
|
311.13
|
622.25
|
1244.51
|
2489.02
|
4978.03
|
9956.06
|
|
E
|
20.60
|
41.20
|
82.41
|
164.81
|
329.63
|
659.26
|
1318.51
|
2637.02
|
5274.04
|
10548.08
|
|
F
|
21.83
|
43.65
|
87.31
|
174.61
|
349.23
|
698.46
|
1396.91
|
2793.83
|
5587.65
|
11175.30
|
|
F#/Gb
|
23.12
|
46.25
|
92.50
|
185.00
|
369.99
|
739.99
|
1479.98
|
2959.96
|
5919.91
|
11839.82
|
|
G
|
24.50
|
49.00
|
98.00
|
196.00
|
392.00
|
783.99
|
1567.98
|
3135.96
|
6271.93
|
12543.85
|
|
G#/Ab
|
25.96
|
51.91
|
103.83
|
207.65
|
415.30
|
830.61
|
1661.22
|
3322.44
|
6644.88
|
13289.75
|
|
A
|
27.50
|
55.00
|
110.00
|
220.00
|
440.00
|
880.00
|
1760.00
|
3520.00
|
7040.00
|
14080.00
|
|
A#/Bb
|
29.14
|
58.27
|
116.54
|
233.08
|
466.16
|
932.33
|
1864.66
|
3729.31
|
7458.62
|
14917.24
|
|
B
|
30.87
|
61.74
|
123.47
|
246.94
|
493.88
|
987.77
|
1975.53
|
3951.07
|
7902.13
|
15804.27
|
Calcolo
di un intervallo a partire dalla frequenza
Cosa fare se ho la frequenza di un suono, supponiamo 100
Hz e voglio sapere, per es., quale frequenza ha la sua
5a? Qui le cose si complicano: vuoi sapere la frequenza
della quinta secondo quale scala?
Come sapete, pur basandosi sempre sul'ottava, nella
storia sono state proposte varie scale. Se consideriamo
la scala temperata, è sufficiente sapere che ogni
semitono sta in un rapporto pari a radice 12ma di 2
(cioè 2 elevato a 1/12 = 1.0594631) con il precedente.
Di conseguenza, per arrivare alla 5a, basta passare per
tutti i 7 semitoni:
100 * 1.0594631 = 105.9463 = 2a min
105.9463 * 1.0594631 = 112.2462 = 2a magg
112.2462 * 1.0594631 = 118.9207 = 3a min, e così via
fino alla 5a che risulta essere 149.8307 Hz.
Più rapidamente, lo stesso valore si calcola come 100 *
1.0594631
7 (cioè 1.0594631 elevato alla 7ma
potenza che è il numero dei semitoni che separano la
tonica dalla 5a); per coloro a cui difettasse la memoria
sull'aritmetica, PRIMA si eleva, POI si moltiplica).
Quindi, in generale, per calcolare un intervallo in Hz,
basta fare
freq
di partenza * 1.0594631numero_semitoni
NB: il calcolo veramente esatto sarebbe
freq di partenza * 2numero_semitoni/12
ma la differenza è questione di qualche decimale, per
cui potete usare la formula di cui sopra.

Diverso è il caso in cui si vuole sapere
la frequenza corrispondente alla 5a giusta, cioè basata
sulla scala degli armonici. Notate che questo caso è
comune in musica elettronica perché spesso si
sovrappongono più suoni per costruirne uno complesso,
per cui le loro frequenze devono essere intonate sugli
armonici (come in natura), non sulla scala temperata.
Per calcolare la frequenza di un intervallo basandosi
sugli armonici, occorre, per prima cosa, identificare
l'armonico che corrisponde a quell'intervallo
servendosi, per es., dell'immagine a fianco o di una
simile.
Da qui si vede che la prima 5a che incontriamo
corrisponde alla componente armonica num. 3 (si conta
anche la fondamentale).
A questo punto si moltiplica la nostra freq. base (per
es. 100 Hz) per tale numero: 100 * 3 = 300, ma
attenzione, questa è la 5a di una ottava superiore. Lo
vediamo perché sappiamo che l'8va di 100 è 200, cioè il
doppio (vedi ancora CDROM di acustica). Quindi dobbiamo
far scendere questa nota di 8va, dividendo per 2 finché
non rientra nell'8va base, cioè finché non è minore di
200. Ora 300 / 2 = 150 che è minore di 200. 150 Hz,
quindi, è la frequenza che cerchiamo.
Altro esempio: sempre partendo da 100 Hz, troviamo la
frequenza della 3a maggiore:
si trova la prima 3a magg. che è la componente num. 5
si calcola la sua frequenza: 100 * 5 = 500
si divide per 2 finché non rientra nell'intervallo di 8a
100 - 200: 500 / 2 = 250 ancora fuori; 250 / 2 = 125 OK!
Notate, per inciso, che la 3a magg. temperata ha invece
frequenza 125.9921 Hz (quasi 1 Hz di differenza). Ecco
una tabella degli intervalli
Intervallo
|
Temp.
equabile
|
Scala
Pitagorica
|
Rapporto
Pitagorico
|
2a
|
1.1224
|
1.1250
|
9/8
|
3a
|
1.26
|
1.25
|
5/4
|
4a
|
1.3348
|
1.333
|
4/3
|
5a
|
1.4983
|
1.5
|
3/2
|
6a
|
1.6818
|
1.6667
|
5/3
|
 L'uomo, all'inizio,
costruisce sempre macchine concettualmente antropomorfe che
riproducono alcune delle sue funzioni. Anche in questo caso, i
primi apparecchi per registrare le onde audio riproducono le
funzioni dell'orecchio. Il nostro sistema percettivo insegna che
l'onda acustica, indirizzata da un apposito canale (padiglione e
canale auricolare) su una membrana (timpano), mette in vibrazione
quest'ultima che, a sua volta, trasmette la vibrazione a una
catena di oggetti rigidi (catena degli ossicini).
L'uomo, all'inizio,
costruisce sempre macchine concettualmente antropomorfe che
riproducono alcune delle sue funzioni. Anche in questo caso, i
primi apparecchi per registrare le onde audio riproducono le
funzioni dell'orecchio. Il nostro sistema percettivo insegna che
l'onda acustica, indirizzata da un apposito canale (padiglione e
canale auricolare) su una membrana (timpano), mette in vibrazione
quest'ultima che, a sua volta, trasmette la vibrazione a una
catena di oggetti rigidi (catena degli ossicini).
 In realtà il fonoautografo non era in grado
di riprodurre le onde sonore, ma solo di inciderle. Edison fu il
primo a fabbricare un apparecchio capace di eseguire entrambi i
compiti: il "fonografo". Nell'immagine a sinistra potete vedere i
solchi incisi da un fonografo di Edison sul supporto di stagno
(ingranditela cliccandoci sopra: è molto grande) e qui potete
sentire la voce di Edison incisa
con uno dei suoi apparecchi. A destra, invece, vedete il modello
di Berliner (successivo) che incideva un disco al posto del
cilindro (anche questa è ingrandibile). Quest'ultimo fu il primo
ad arrivare alla produzione di massa nel 1888 con un disco di 7
pollici (17.78 cm) che girava a 30 giri/min. (solo 2 min di durata
perché i solchi erano larghi e distanziati fra loro).
In realtà il fonoautografo non era in grado
di riprodurre le onde sonore, ma solo di inciderle. Edison fu il
primo a fabbricare un apparecchio capace di eseguire entrambi i
compiti: il "fonografo". Nell'immagine a sinistra potete vedere i
solchi incisi da un fonografo di Edison sul supporto di stagno
(ingranditela cliccandoci sopra: è molto grande) e qui potete
sentire la voce di Edison incisa
con uno dei suoi apparecchi. A destra, invece, vedete il modello
di Berliner (successivo) che incideva un disco al posto del
cilindro (anche questa è ingrandibile). Quest'ultimo fu il primo
ad arrivare alla produzione di massa nel 1888 con un disco di 7
pollici (17.78 cm) che girava a 30 giri/min. (solo 2 min di durata
perché i solchi erano larghi e distanziati fra loro).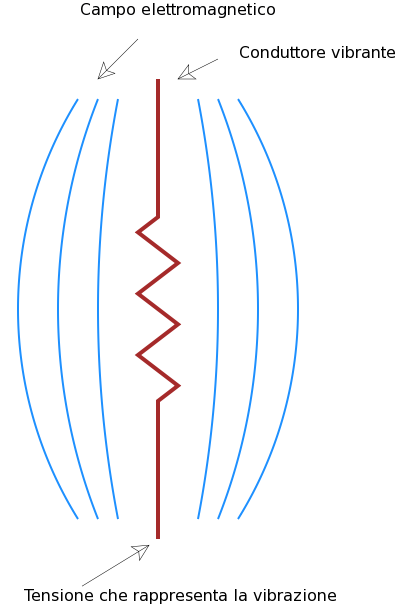
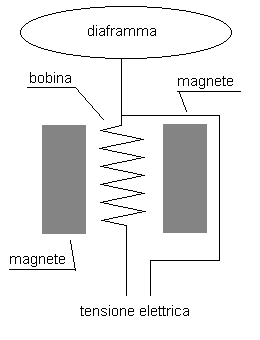 Visto il principio di cui
sopra, è facile capire come può essere fatto un microfono.
Visto il principio di cui
sopra, è facile capire come può essere fatto un microfono.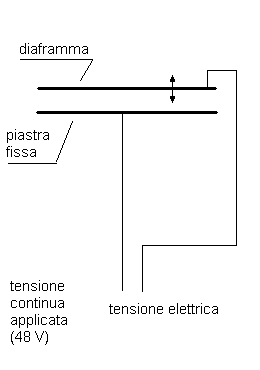 Oggi esistono
diversi tipi di microfoni dinamici, che si differenziano
moltissimo in base alla qualità (da pochi Euro, come i microfoni
forniti di serie con le schede audio più comuni, e adatti per
applicazioni vocali) fino a centinaia di Euro, adatti per
applicazioni musicali. Fra le caratteristiche dei microfoni
dinamici si può ancora citare la relativa insensibilità ai rumori
meccanici esterni (come il maneggiamento del microfono) e lo
spiccato effetto di prossimità, cioè la caratteristica di variare
la risposta in frequenza, e quindi la timbrica, a seconda della
distanza del microfono dalla sorgente sonora. I microfoni dinamici
sopportano, generalmente, elevate pressioni acustiche.
Oggi esistono
diversi tipi di microfoni dinamici, che si differenziano
moltissimo in base alla qualità (da pochi Euro, come i microfoni
forniti di serie con le schede audio più comuni, e adatti per
applicazioni vocali) fino a centinaia di Euro, adatti per
applicazioni musicali. Fra le caratteristiche dei microfoni
dinamici si può ancora citare la relativa insensibilità ai rumori
meccanici esterni (come il maneggiamento del microfono) e lo
spiccato effetto di prossimità, cioè la caratteristica di variare
la risposta in frequenza, e quindi la timbrica, a seconda della
distanza del microfono dalla sorgente sonora. I microfoni dinamici
sopportano, generalmente, elevate pressioni acustiche. 
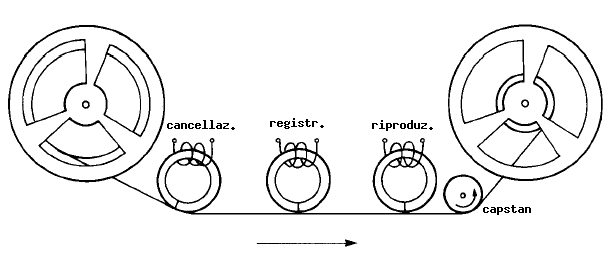 Lo schema di funzionamento
di un registratore a nastro è il seguente: il registratore è
sostanzialmente costituito da un sistema di trascinamento che ha
lo scopo di far scorrere il nastro ad una velocità costante di
fronte a tre "testine magnetiche" usate, rispettivamente, per la
registrazione, la cancellazione e la riproduzione.
Lo schema di funzionamento
di un registratore a nastro è il seguente: il registratore è
sostanzialmente costituito da un sistema di trascinamento che ha
lo scopo di far scorrere il nastro ad una velocità costante di
fronte a tre "testine magnetiche" usate, rispettivamente, per la
registrazione, la cancellazione e la riproduzione.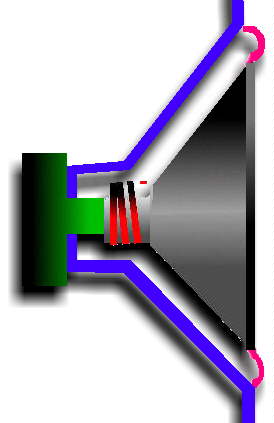
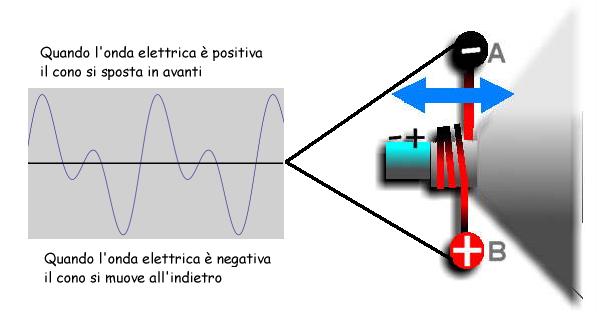 In tal modo, il
cono vibra seguendo l'andamento della corrente e muove l'aria
davanti a sè riproducendo l'onda acustica. Se, per esempio, si
applica una variazione con una frequenza di 1000 Hz (mille cicli
al secondo) il cono si sposterà avanti e indietro 1000 volte al
secondo, e quindi produrrà una frequenza udibile di 1000 Hz. Se viene immesso un segnale con una corrente
alternata a 3000 Hz, ecco che l'altoparlante riprodurrà un
suono di 3000 Hz.
In tal modo, il
cono vibra seguendo l'andamento della corrente e muove l'aria
davanti a sè riproducendo l'onda acustica. Se, per esempio, si
applica una variazione con una frequenza di 1000 Hz (mille cicli
al secondo) il cono si sposterà avanti e indietro 1000 volte al
secondo, e quindi produrrà una frequenza udibile di 1000 Hz. Se viene immesso un segnale con una corrente
alternata a 3000 Hz, ecco che l'altoparlante riprodurrà un
suono di 3000 Hz.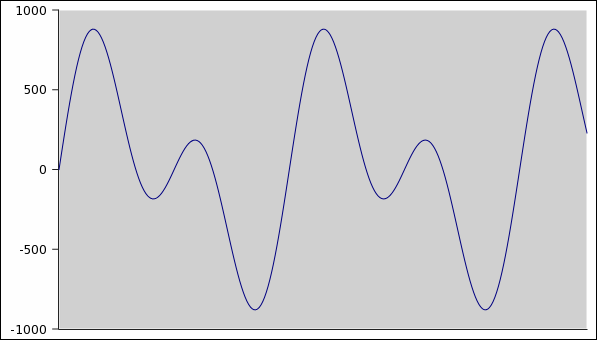
 Osservate la figura a sinistra.
Osservate la figura a sinistra.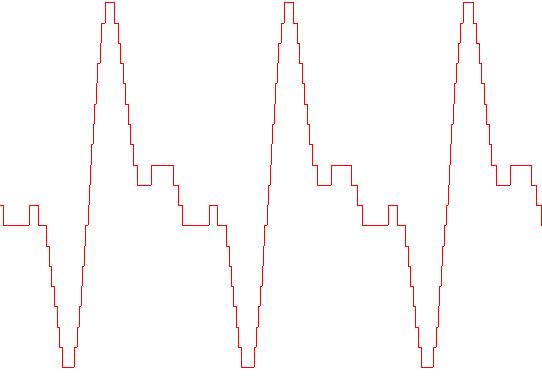
 Ma calma, vediamo un esempio. Il Do più alto del piano che, a parte qualche caso sporadico, possiamo considerare come la fondamentale più alta nella nostra musica, è 4186 Hz. Se semplicemente andiamo al La della penultima 8va del piano che è 1760 Hz, il nostro spettro va in foldover già alla 13ma componente. Andando su di un'altra 8va siamo a 3520 che va in foldover alla 7ma componente e
Ma calma, vediamo un esempio. Il Do più alto del piano che, a parte qualche caso sporadico, possiamo considerare come la fondamentale più alta nella nostra musica, è 4186 Hz. Se semplicemente andiamo al La della penultima 8va del piano che è 1760 Hz, il nostro spettro va in foldover già alla 13ma componente. Andando su di un'altra 8va siamo a 3520 che va in foldover alla 7ma componente e 

 Diverso è il caso in cui si vuole sapere
la frequenza corrispondente alla 5a giusta, cioè basata
sulla scala degli armonici. Notate che questo caso è
comune in musica elettronica perché spesso si
sovrappongono più suoni per costruirne uno complesso,
per cui le loro frequenze devono essere intonate sugli
armonici (come in natura), non sulla scala temperata.
Diverso è il caso in cui si vuole sapere
la frequenza corrispondente alla 5a giusta, cioè basata
sulla scala degli armonici. Notate che questo caso è
comune in musica elettronica perché spesso si
sovrappongono più suoni per costruirne uno complesso,
per cui le loro frequenze devono essere intonate sugli
armonici (come in natura), non sulla scala temperata.