Nota: gli esempi sonori linkati nel testo sono stati compressi in MP3 non tanto per risparmiare spazio (la compressione è a bitrate 320, la minima possibile), ma perché ho notato che alcuni browser hanno qualche difficoltà nel leggere i file wav e aiff via link, mentre tutti leggono senza problemi gli mp3.
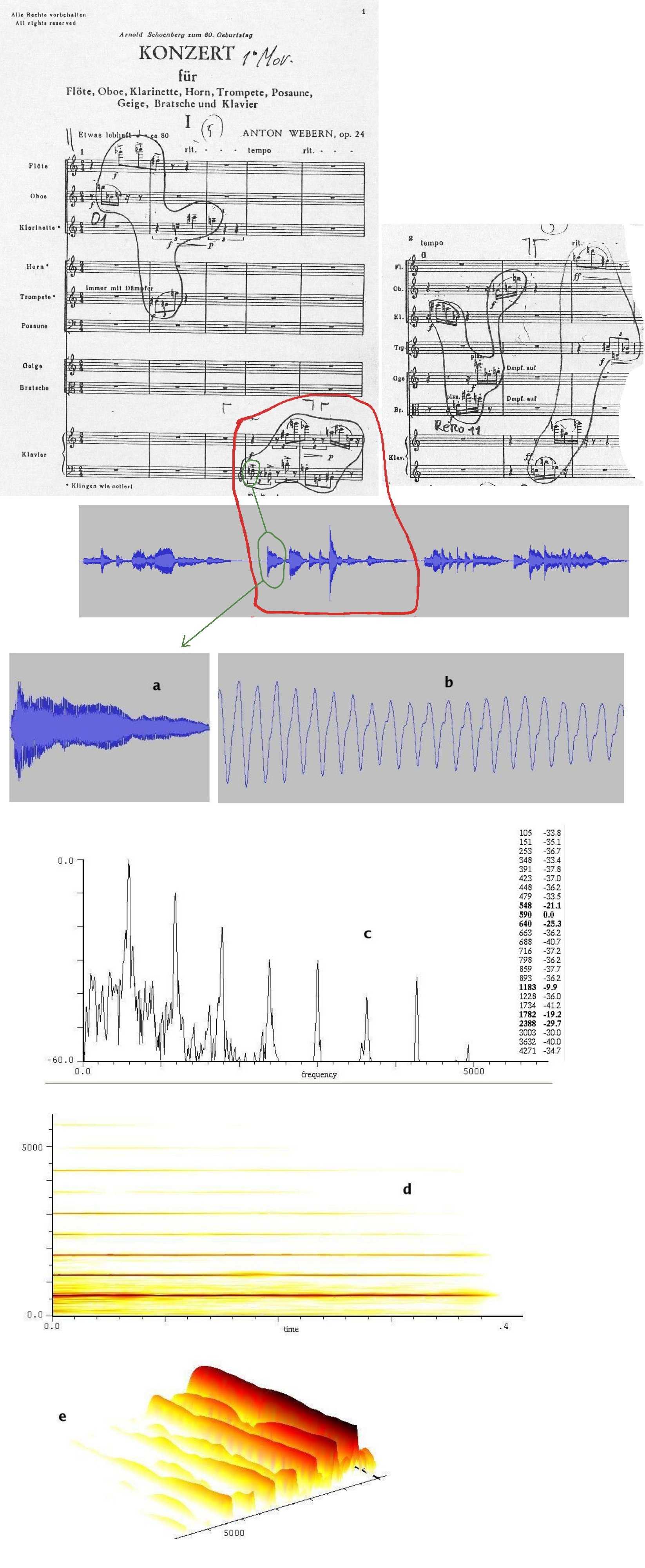
In questa figura è schematizzato il passaggio dalla musica all'analisi del singolo suono. È importante osservare che, fino al riquadro b passiamo attraverso vari livelli di ingrandimento del fenomeno sonoro: da c in poi, invece, passiamo all'analisi.

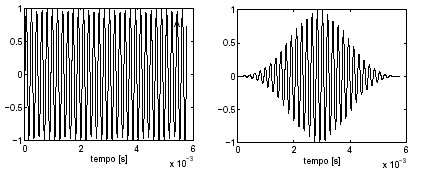
Si tratta di questa brevissima nota di pianoforte (Re4) vista:
La tecnica utilizzata in queste analisi è la FFT (fast fourier transform: trasformata veloce di Fourier) che è la versione ottimizzata per massimizzare la velocità di calcolo su computer della DFT (discrete fourier transform: trasformata discreta di Fourier).
La base della FFT è il fatto che ogni segnale può essere scomposto in una serie di sinusoidi, ciascuna delle quali possiede una ben determinata frequenza, ampiezza e fase (trasformata di Fourier).
Bisogna notare che la trasformata di Fourier non è l'unica esistente. Esistono altre trasformate in grado di scomporre un segnale in una serie di componenti dello stesso tipo. Quella di Walsh, per esempio, scompone un segnale in una serie di onde quadre e presenta dei vantaggi dal punto di vista della sintesi (le onde quadre sono molto più facili da generare rispetto alle sinusoidi). La trasformata di Fourier, però, evidenzia alcune caratteristiche interessanti:
Con la FFT, quindi, possiamo analizzare lo spettro di un suono e vedere le sue componenti, siano esse armoniche o meno, passando dalla visione della forma d'onda, con il tempo sull'asse X, alla visione in frequenza (frequenze sull'asse X). Proprio per questo è corretto dire che, con la FFT, si passa dal dominio del tempo a quello della frequenza.
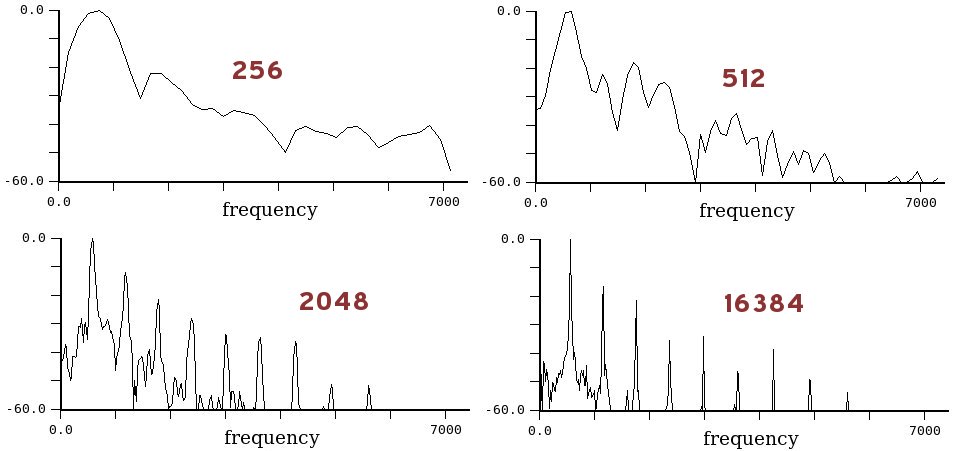
Il principale parametro di controllo della FFT è la sua risoluzione che è determinata dal numero di campioni (detti "punti") su cui viene effettuata. Come vedete nella figura seguente, le componenti (o parziali) della nota di pianoforte di cui sopra sono via via più evidenti con l'aumentare del numero di punti. Naturalmente un maggior numero di punti significa anche un maggior tempo di calcolo che, con i computer di oggi, è, comunque, minimo.
Si ha, quindi, un passaggio dal dominio del tempo a quello delle frequenze. Come tale, però, la FFT è una analisi istantanea che vale solamente in quel punto del suono. Dato che il suono è in evoluzione, potete considerare una singola FFT come un fotogramma di un film.
Ovvero si fa una sola analisi su un frammento del suono di lunghezza pari al numero dei punti usato nell'analisi, il che restituisce l'immagine di un singolo spettro
Dal punto di vista acustico la FFT può benissimo essere vista come un semplice banco di filtri che suddivide l'intero spazio delle frequenze, da 0 a SR/2, in tante bande quanti sono i punti diviso 2. Una FFT a 1024 punti, quindi, equivale a suddividere il campo frequenziale in 512 bande.
Per ognuna di queste bande la FFT restituisce l'ampiezza (e darebbe anche la fase che, di solito, viene ignorata dai software di elaborazione audio, con la scusa che il nostro sistema percettivo è insensibile alla fase, ma, in realtà, averla non sarebbe del tutto inutile). Comunque, se, per esempio, si lavora con 2048 punti, è come se si dividesse l'intero spazio frequenziale, che va da 0 a SR/2, in 2048/2 = 1024 bande.
La formula per calcolare la larghezza da ogni banda è SR/2 diviso numero_punti/2 e dato che il "/2" è presente in entrambi i valori, possiamo eliminarlo. Quindi abbiamo
numero bande = numero_punti su cui si effettua l'analisi / 2
larghezza di ogni banda = SR / numero punti su cui si effettua l'analisi
In definitiva, con SR = 44100 e numero_punti = 2048, abbiamo 1024 bande la cui larghezza è 44100/2048 = 21.533203125 Hz.
Vedendo la cosa in questo modo, si capisce anche perché la risoluzione in frequenza aumenta con il numero dei punti e quindi anche perché, nella figura qui sopra, con 256 punti non si isolano le componenti. La larghezza di banda è 44100/256 = 172.265625 Hz, che è troppo per isolare delle singole sinusoidi. La situazione migliora un po' con 512 punti (larghezza di banda 86.1328125 Hz), è ancora migliore con 2048 (larg. 21.533203125 Hz), buona con 4096 (larg. circa 10.7666 Hz), molto buona con 8192 (larg. 5.38330078125 Hz) e ottima con 16384 punti (larg. circa 2.69165 Hz) e superiori (con 65536 punti si arriva a una larghezza di banda pari a 0.67291259765625 Hz).
Però in questi ultimi casi, bisogna anche considerare l'aspetto temporale. Con SR 44100, 16384 punti sono quasi 4 decimi di secondo (0.371519274376417), 32768 punti sono più di 7 decimi (0.743038548752834) e 65536 sono addirittura >1.486 secondi e se nel segmento di analisi il suono cambia radicalmente si corre il rischio è di falsare totalmente i risultati. Ovviamente più lungo è il segmento di analisi più probabilità ci sono che il suono non sia fisso.
 La seconda cosa da ricordare, a questo punto, è che, come già detto, una singola analisi la dimensione tempo non esiste. I dati che escono rappresentano in x le frequenze delle bande e in y la loro ampiezza (vedi esempio qui sotto). Il tempo non c'è. L'analisi che mostra un singolo spettro è istantanea cioè vale solo per l'istante in cui è stata effettuata. Il punto di analisi è quello mediano rispetto al segmento analizzato. Se abbiamo un suono con SR = 44100 e facciamo una analisi su 4096 punti, che a SR 44100 corrispondono quasi a 1/10 di secondo (≈0.09 sec.), l'istante a cui l'analisi si riferisce è il centro di quei 4096 campioni. Prima e dopo, il suono potrebbe essere diverso.
La seconda cosa da ricordare, a questo punto, è che, come già detto, una singola analisi la dimensione tempo non esiste. I dati che escono rappresentano in x le frequenze delle bande e in y la loro ampiezza (vedi esempio qui sotto). Il tempo non c'è. L'analisi che mostra un singolo spettro è istantanea cioè vale solo per l'istante in cui è stata effettuata. Il punto di analisi è quello mediano rispetto al segmento analizzato. Se abbiamo un suono con SR = 44100 e facciamo una analisi su 4096 punti, che a SR 44100 corrispondono quasi a 1/10 di secondo (≈0.09 sec.), l'istante a cui l'analisi si riferisce è il centro di quei 4096 campioni. Prima e dopo, il suono potrebbe essere diverso.
È quindi errato fare una analisi e pensare "in questo suono troviamo queste componenti". Il concetto esatto è "in questo suono, in questo istante, troviamo queste componenti". In effetti, il segmento su cui si fa l'analisi viene dapprima isolato e poi moltiplicato per un inviluppo a forma di campana (con il massimo al centro) come nella figura a fianco. Questo per evitare che il troncamento alle estremità influenzi il risultato. L'effetto della finestra è quello di dare un peso maggiore al centro del segmento e mostrare lo spettro con maggiore pulizia.
Un'altra cosa da tener presente è che la FFT non ci dà le frequenze esatte delle componenti, ma solo le frequenze di inzio e fine delle bande che dipendono dal numero di punti in cui si esegue l'analisi. Per esempio, se nell'analisi trovo una ampiezza notevole nella banda che va da 258.398438 a 263.781738 Hz (8192 punti, risoluzione 5.38330078125 Hz), io capisco che in questa banda c'è qualcosa di significativo, ma la FFT non mi dice cos'è (una sinusoide?, più sinusoidi?, rumore?) né, nel caso sia una sola sinusoide, che frequenza esatta ha, quindi per avere le frequenze precise delle componenti bisogna fare una stima, come vedremo.
Infine, l'ascolto è fondamentale. Possedendo adeguate competenze di acustica, dal semplice ascolto si traggono informazioni che possono semplificare brutalmente una cosa che nell'analisi sembra complicata. Guardate questo grafico:
A guardarlo così sembra quasi lo spettro di un suono inarmonico, anche se, guardando bene, si possono vedere alcune regolarità che fanno pensare a più note insieme. L'ascolto risolve tutto, cliccate qui.
Ok, ammetto di aver giocato un po' sporco, ma questo esempio mostra come una cosa molto banale possa assumere un aspetto molto complicato che un ascolto risolve facilmente. Si dovrebbe sempre iniziare da un ascolto consapevole da cui trarre tutte le informazioni possibili. Vediamo un esempio di analisi.
Ascoltate questo suono. Semplicemente ascoltandolo posso dedurre che:
Ecco l'immagine del suono.
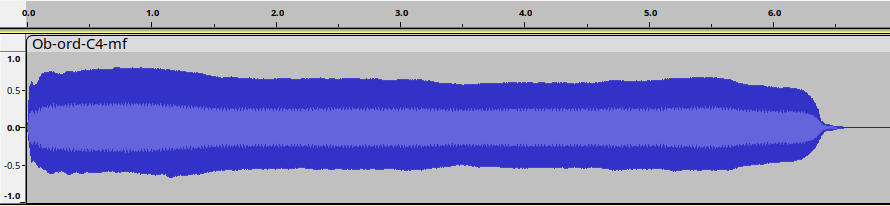
In pratica di lui sappiamo già quasi tutto. Ci mancano solo le ampiezze delle componenti che potremo facilmente ricavare dai dati forniti dalla FFT. C'è, però, una leggera variazione in ampiezza nella parte centrale, su cui è bene indagare per capire quanto potrebbe influire.
Quindi facciamo due FFT singole: una nel punto di ampiezza maggiore e una in quello minore e le confrontiamo. Il risultato è questo
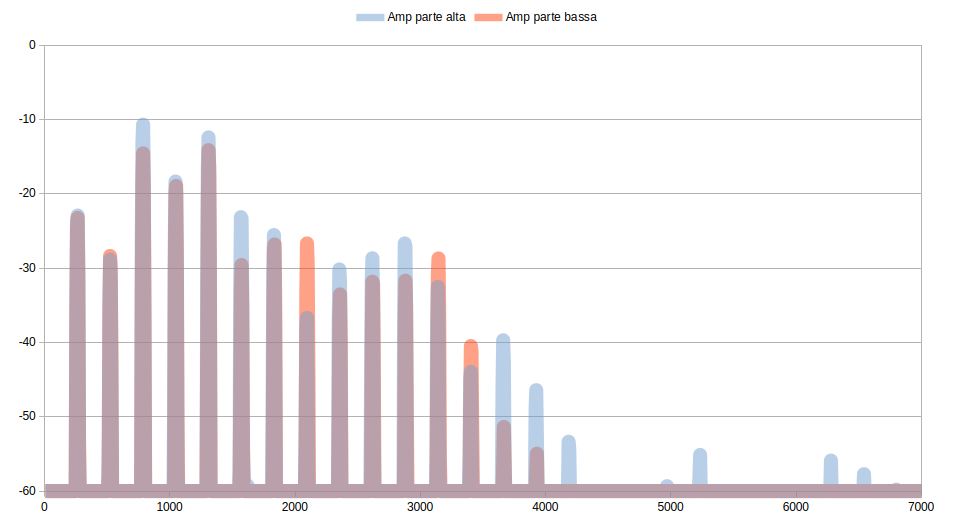
e si legge così: le due ampiezze sono sovrapposte. Dove la barra è grigia, l'ampiezza è uguale; dove una parte azzurra sporge, l'ampiezza misurata nella parte con ampiezza più alta è maggiore di quella misurata nella parte con ampiezza più bassa; dove, invece, sporge una parte arancione è l'inverso.
Da qui si vede che la differenza non è così banale. In molte componenti l'ampiezza misurata dove il segnale è più alto è decisamente superiore a quella della parte con segnale più basso. questo fa pensare che sarebbe meglio avere una media pesata delle ampiezze. Si può fare?
Finora abbiamo parlato di una analisi singola, cioè fatta esattamente sul numero di punti scelto e basta. In effetti la FFT funziona così: fa una analisi esaminando solo il numero di punti scelto. Però normalmente l'utente non fa così. In genere sceglie il numero di punti e poi seleziona una parte del segnale, lunga anche vari secondi e chiede al software di fare la FFT su tutta quella parte.
Ora, le due cose non coincidono. Il numero dei punti scelto è, supponiamo, 8192, ma la parte selezionata è, per esempio, lunga 4 secondi che, a SR 44100, fanno 176400 campioni. Cosa fa il software in questo caso?
Ovviamente dipende da chi ha scritto il software (l'analisi FFT è disponibile in vari software di elaborazione audio), ma normalmente il software fa molte analisi, partendo dall'inizio del blocco selezionato e andando avanti finché non arriva al termine della selezione. Alla fine, per ogni banda, fa una media dei valori di ampiezza.
Normalmente le varie analisi sono in parte sovrapposte in modo da rendere più graduale il passaggio dai valori di un blocco a quelli del successivo, ma, in questo caso, però, il software dovrebbe chiedere all'utente anche il fattore di sovrapposizione, come fa Max nell'oggetto pfft~, cosa che quasi nessun software fa.
Nel nostro caso (numero_punti 8192 e blocco selezionato 176400), se il fattore di sovrapposizione fosse, per es. il 50%, il software dovrebbe fare almeno 42 analisi partendo dall'inizio della selezione e spostandosi in avanti ogni volta di 4096 campioni e alla fine dare la media delle ampiezze per ogni banda.
Inoltre non si tratta di una media semplice, ma di una media pesata in base ai tempi per cui i diversi valori di ampiezza si presentano. Per esempio, supponiamo che, nel caso di 42 analisi che abbiamo ipotizzato qui sopra, l'ampiezza di una certa banda sia 0.8 per 12 analisi e poi scenda a 0.2 per le altre 30. L'ampiezza risultante non sarà semplicemente (0.8+0.2)/2 = 0.5, ma sarà (0.8*12 + 0.2*30)/42 ≈ 0.371428571428571 (il simbolo ≈ in matematica significa uguale circa e si usa, per esempio, quando il risultato è una approssimazione (e.g. avrebbe più decimali di quelli visualizzati)).
Quindi, se si seleziona un blocco di lunghezza superiore a quella del numero_punti della singola FFT, è importante ricordare che l'ampiezza che uscirà per ogni banda sarà una media pesata.
Di conseguenza questa faccenda della media delle ampiezze ha un effetto anche sulle frequenze. Se, nella parte selezionata il segnale cambia in frequenza, tutte le frequenze e le relative componenti risulteranno nello spettro con una certa ampiezza come se fossero presenti per tutta la durata del segnale selezionato. Perché?
È semplice: supponiamo che, nella parte selezionata, il segnale sia a 100 Hz per un certo tempo e poi vada a 180 Hz. Il software vede una attività e quindi una ampiezza nella banda che contiene i 100 Hz per un certo numero di analisi. Poi da questa banda il segnale scompare, quindi l'ampiezza va a zero, ma appare nella banda dei 180 Hz. Alla fine entrambe queste bande avranno dei valori di ampiezza in alcune analisi e in altre avranno zero, ma, facendo la media, risulterà un valore ≠ 0 perché nel singolo spettro non c'è la dimensione temporale.
Quindi, se il risultato dell'analisi è la rappresentazione di un solo spettro, è bene evitare di selezionare parti del segnale in cui la frequenza cambia.
Ultima considerazione: la FFT si fa su segnali monofonici. Se un suono è stereo, l'unica possibilità è farne due, una per canale o, meglio, renderlo monofonico sommando i due canali con il 50% di ampiezza.
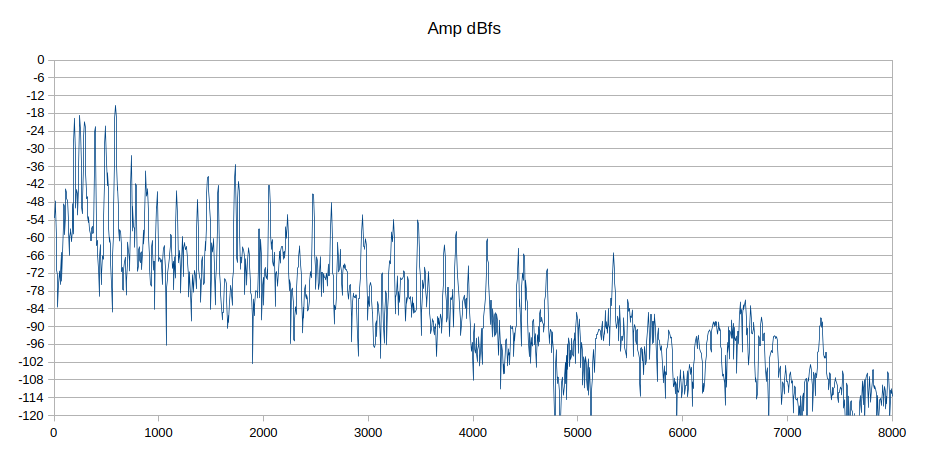
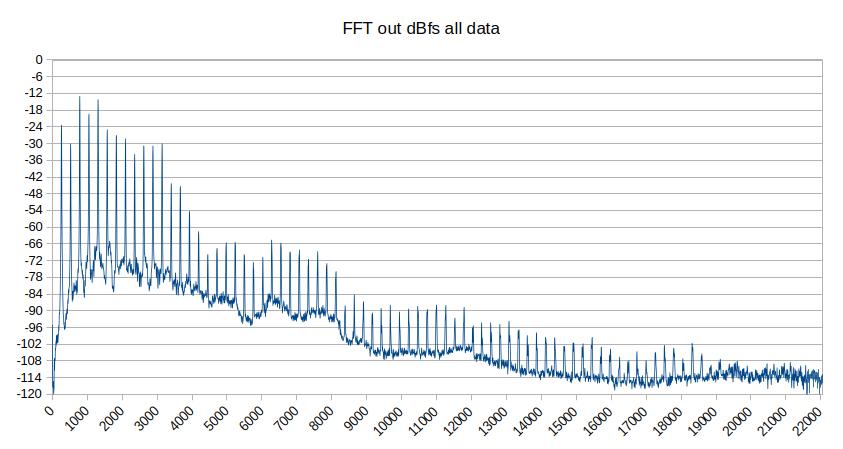
Questo è il grafico dei dati in uscita dalla FFT con ampiezze in dBfs. L'area selezionata per l'analisi è buona parte del sustain, in modo da escludere l'attacco e il decay. Notate che per ora non mi interessa riprodurre esattamente tutto l'andamento del suono, ma solo ottenere una sonorità uguale e mostrare come si possa fare grazie alla FFT.
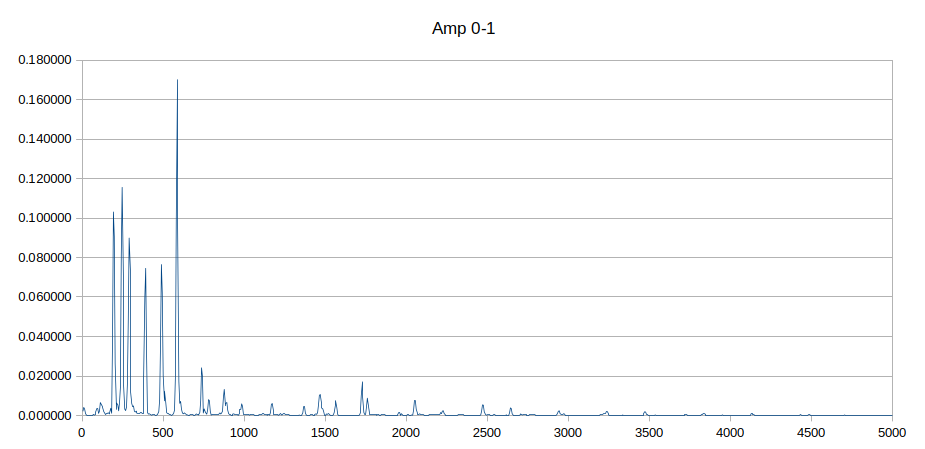
E questo in ampiezza assoluta 0-1 (area come sopra).
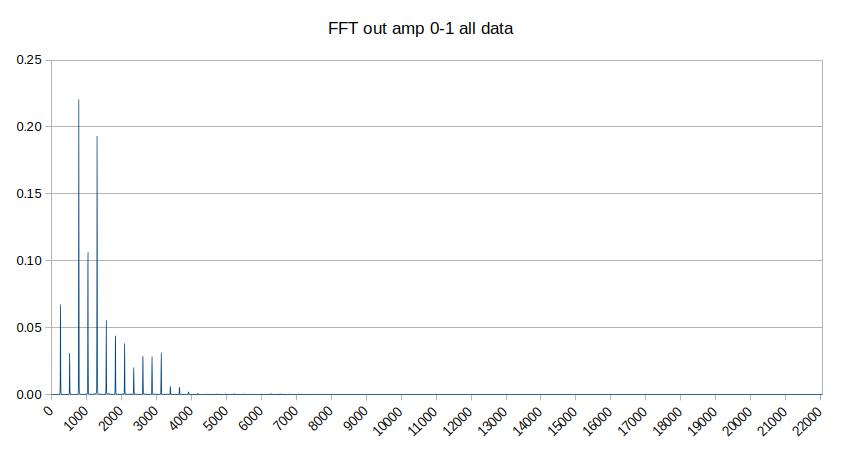
Può sembrare strano che, rispetto all'immagine in dBfs, scompaiano anche i picchi fra 5000 e 8000 Hz che arrivano a -66 dBfs, ma pensate che -66 dBfs convertiti in amp 0-1 sono inferiori a 0.0005 cioè 5 decimillesimi del massimo. In realtà anche nel grafico in ampiezza assoluta ci sono, ma sono così piccoli che coprono al massimo 1 o 2 pixel. Se si ingrandisce molto l'immagine si vedono.
Queste sono le formule di conversione fra dBfs e Amp 0-1 e ovviamente l'una è l'inverso dell'altra:
N.B. c'è una differenza fra potenza acustica e pressione sonora (non a caso quest'ultima si indica con deciBelSPL dove SPL sta per sound pressure level): la pressione sonora è più significativa della potenza perché rappresenta la pressione media che si esercita sul timpano ed è questa che viene rilevata dal nostro sistema percettivo. Quando si misura l'intensità percepita di un segnale esterno, cioè quello emesso da qualcosa (un altoparlante, uno strumento, un'auto, un aereo, etc), si misura la pressione sonora, non la potenza acustica e per questo si parla di deciBelSPL. La pressione sonora è legata all'ambiente e soprattutto alla distanza. La potenza acustica, invece, è l'energia totale emessa da una sorgente in un secondo (misurata in Watt). È una quantità assoluta e oggettiva che descrive la potenza della sorgente ed è indipendente dall'ambiente circostante e dalla distanza.
Alla fine, per la risintesi si può scegliere il sistema più adeguato. Nel caso di questo suono, la sintesi additiva è, ovviamente, il sistema più adatto però, essendo il suono formato da componenti armoniche, potremmo anche usare una singola wavetable.
Per esempio questa è la risintesi con una wavetable singola: sentite prima il suono originale (7 sec.), poi la rintesi (3 sec.).
N.B.: Attenzione ai malefici speakers del computer. Se ascoltate con gli speakers del computer, abbassate il volume sul computer perché spesso, se l'ampiezza è alta, introducono una leggera distorsione che fa sembrare un suono più brillante dell'altro (in questo caso quello sintetizzato perché è ad ampiezza fissa rispetto all'altro). Diffidate delle cuffiette: spesso i bassi scompaiono. Meglio collegare l'out del computer a un impianto esterno oppure a una buona scheda audio o a una vera cuffia. Inoltre, ascoltando via browser cliccando il link, parte il player del browser sempre a volume massimo e bisogna abbassarlo per avere una riproduzione fedele. (ho provato con Firefox, Chromium e Opera e il problema è comune).
Ho fatto 5 analisi FFT con software diversi e alla fine ho scelto questa. La seconda è meno brillante. Nelle altre ci sono lievi differenze, soprattutto sugli armonici più lontani. Comunque sono tutte molto simili. Le potete ascoltare qui sempre con l'originale all'inizio per circa 7 secondi.
Per ottenere i dati per produrre la risintesi da quelli in uscita dalla FFT occorre, però, lavorare un po'. In questo caso ho selezionato solo la fase di sustain del suono escludendo l'attacco e il release. L'analisi è stata fatta su 8192 punti, quindi ogni banda era larga 5.38330078125 Hz. La FFT ha fatto una serie di analisi coprendo tutta parte selezionata e mi dato 4096 bande con frequenza iniziale e relativa ampiezza con le quali ho creato, in un foglio elettronico, una tabella di 4096 righe a partire dalla quale, sapendo che il suono analizzato era armonico, ho selezionato i dati di quella trentina di componenti che vedete nelle figure qui sopra.
Per fare questo, ho usato lo spreadsheet per fare un po' di calcoli sull'intera massa di dati, aggiungendo altre 6 colonne.
Qui sotto allego parte della tabella che contiene i dati in uscita da una FFT e mostra le elaborazioni che faccio per individuare le componenti più significative (la tabella completa è di 4096 righe; qui metto solo le prime 200 sufficienti per capire i calcoli che sono ripetuti uguali su ogni riga).
Prima di esaminare la tabella è necessario assicurarsi di conoscere alcuni dati:
Quindi ripassiamo un po' di formule
Questi sono i grafici in dBfs e Amp 0-1 ricavati dai dati esportati dalla FFT.


A questo punto vediamo la tabella e i calcoli che faccio sui valori in uscita dall'FFT.
Quello che vedete in tabella è parte di uno spreadsheet programmato da me per semplicarmi il lavoro. Se lo facessi a mano dovrei cercare tutti gli spikes che vedete nei grafici fra le 4096 righe della tabella. Meglio farlo fare al computer.
Qui vedete parte della tabella. Le prime due colonne, in verde, sono i dati che arrivano dalla FFT. Tutte le celle in nero sono calcolate in base alle mie istruzioni. Le celle in rosso sono valori che io devo dare e si basano su mie valutazioni.
Le spiegazioni sono sotto la tabella.
| Mauro | FFT study | min dBfs | -268.077271 | Resc fact | min lev | fond | ||
| Graziani | max dBfs | -13.083014 | 13.083014 | -65 | 262.000 | |||
| min Amp | 0.000000 | |||||||
| max Amp | 0.220599 | 4.533114 | ||||||
| Freq Hz | Amp dBfs | Amp 0-1 | Resc dBfs | Resc 0-1 | > min lev |
Peaks | Ratio | |
| 0 | -268.077270508 | 0.000000 | -254.994256 | 0.000000 | ||||
| 5.383 | -92.325828552 | 0.000023 | -79.242814 | 0.000106 | ||||
| 10.766 | -102.850219727 | 0.000007 | -89.767205 | 0.000031 | ||||
| 16.149 | -115.531333923 | 0.000002 | -102.448319 | 0.000007 | ||||
| 21.533 | -116.229446411 | 0.000001 | -103.146432 | 0.000007 | ||||
| 26.916 | -114.866897583 | 0.000002 | -101.783883 | 0.000008 | ||||
| 32.299 | -116.199882507 | 0.000001 | -103.116868 | 0.000007 | ||||
| 37.683 | -118.445617676 | 0.000001 | -105.362603 | 0.000005 | ||||
| 43.066 | -117.815132141 | 0.000001 | -104.732118 | 0.000006 | ||||
| 48.449 | -114.052764893 | 0.000002 | -100.969750 | 0.000009 | ||||
| 53.833 | -108.135032654 | 0.000004 | -95.052018 | 0.000017 | ||||
| 59.216 | -106.44090271 | 0.000005 | -93.357888 | 0.000021 | ||||
| 64.599 | -108.175949097 | 0.000004 | -95.092935 | 0.000017 | ||||
| 69.982 | -107.14025116 | 0.000004 | -94.057237 | 0.000019 | ||||
| 75.366 | -106.546028137 | 0.000005 | -93.463014 | 0.000020 | ||||
| 80.749 | -105.438941956 | 0.000005 | -92.355927 | 0.000023 | ||||
| 86.132 | -102.994018555 | 0.000007 | -89.911004 | 0.000031 | ||||
| 91.516 | -102.981643677 | 0.000007 | -89.898629 | 0.000031 | ||||
| 96.899 | -101.906089783 | 0.000008 | -88.823075 | 0.000035 | ||||
| 102.282 | -100.164474487 | 0.000009 | -87.081460 | 0.000043 | ||||
| 107.666 | -100.175422668 | 0.000009 | -87.092408 | 0.000043 | ||||
| 113.049 | -98.759178162 | 0.000011 | -85.676164 | 0.000050 | ||||
| 118.432 | -98.068893433 | 0.000012 | -84.985879 | 0.000054 | ||||
| 123.815 | -99.21308136 | 0.000011 | -86.130067 | 0.000048 | ||||
| 129.199 | -99.943199158 | 0.000010 | -86.860185 | 0.000044 | ||||
| 134.582 | -98.973274231 | 0.000011 | -85.890260 | 0.000049 | ||||
| 139.965 | -98.093109131 | 0.000012 | -85.010095 | 0.000054 | ||||
| 145.349 | -97.914115906 | 0.000012 | -84.831101 | 0.000055 | ||||
| 150.732 | -99.506561279 | 0.000010 | -86.423547 | 0.000046 | ||||
| 156.115 | -100.254898071 | 0.000009 | -87.171884 | 0.000042 | ||||
| 161.499 | -99.712715149 | 0.000010 | -86.629701 | 0.000045 | ||||
| 166.882 | -99.290863037 | 0.000010 | -86.207849 | 0.000047 | ||||
| 172.265 | -98.427482605 | 0.000012 | -85.344468 | 0.000052 | ||||
| 177.648 | -97.359855652 | 0.000013 | -84.276841 | 0.000059 | ||||
| 183.032 | -95.883293152 | 0.000015 | -82.800279 | 0.000070 | ||||
| 188.415 | -95.211738586 | 0.000017 | -82.128724 | 0.000076 | ||||
| 193.798 | -93.476852417 | 0.000020 | -80.393838 | 0.000093 | ||||
| 199.182 | -91.817962646 | 0.000025 | -78.734948 | 0.000112 | ||||
| 204.565 | -91.696006775 | 0.000025 | -78.612992 | 0.000114 | ||||
| 209.948 | -93.609153748 | 0.000020 | -80.526139 | 0.000091 | ||||
| 215.332 | -93.602127075 | 0.000020 | -80.519113 | 0.000091 | ||||
| 220.715 | -91.45539093 | 0.000026 | -78.372376 | 0.000117 | ||||
| 226.098 | -87.631858826 | 0.000040 | -74.548844 | 0.000182 | ||||
| 231.481 | -83.942520142 | 0.000061 | -70.859506 | 0.000279 | ||||
| 236.865 | -83.122550964 | 0.000068 | -70.039536 | 0.000306 | ||||
| 242.248 | -79.369865417 | 0.000104 | -66.286851 | 0.000472 | ||||
| 247.631 | -49.009960175 | 0.003476 | -35.926946 | 0.015757 | 247.631 | 0.945 | ||
| 253.015 | -32.023845673 | 0.024735 | -18.940831 | 0.112126 | 253.015 | 0.966 | ||
| 258.398 | -24.082872391 | 0.061904 | -10.999858 | 0.280620 | 258.398 | 0.986 | ||
| 263.781 | -23.102313995 | 0.069330 | -10.019300 | 0.314279 | 263.781 | 263.781 | 1.007 | |
| 269.165 | -28.874334335 | 0.035590 | -15.791320 | 0.161333 | 269.165 | 1.027 | ||
| 274.548 | -42.774040222 | 0.007144 | -29.691026 | 0.032386 | 274.548 | 1.048 | ||
| 279.931 | -70.293167114 | 0.000297 | -57.210153 | 0.001348 | ||||
| 285.314 | -91.589080811 | 0.000025 | -78.506066 | 0.000115 | ||||
| 290.698 | -93.77747345 | 0.000020 | -80.694459 | 0.000089 | ||||
| 296.081 | -94.604240417 | 0.000018 | -81.521226 | 0.000081 | ||||
| 301.464 | -96.519432068 | 0.000014 | -83.436418 | 0.000065 | ||||
| 306.848 | -98.050346374 | 0.000012 | -84.967332 | 0.000055 | ||||
| 312.231 | -96.534034729 | 0.000014 | -83.451020 | 0.000065 | ||||
| 317.614 | -93.390510559 | 0.000021 | -80.307496 | 0.000094 | ||||
| 322.998 | -92.537605286 | 0.000023 | -79.454591 | 0.000103 | ||||
| 328.381 | -94.715827942 | 0.000018 | -81.632813 | 0.000080 | ||||
| 333.764 | -95.486419678 | 0.000016 | -82.403405 | 0.000073 | ||||
| 339.147 | -94.541824341 | 0.000018 | -81.458810 | 0.000082 | ||||
| 344.531 | -95.224830627 | 0.000017 | -82.141816 | 0.000076 | ||||
| 349.914 | -95.389442444 | 0.000016 | -82.306428 | 0.000074 | ||||
| 355.297 | -94.831443787 | 0.000017 | -81.748429 | 0.000079 | ||||
| 360.681 | -95.172798157 | 0.000017 | -82.089784 | 0.000076 | ||||
| 366.064 | -95.358169556 | 0.000016 | -82.275155 | 0.000074 | ||||
| 371.447 | -94.090705872 | 0.000019 | -81.007691 | 0.000086 | ||||
| 376.831 | -92.604133606 | 0.000023 | -79.521119 | 0.000102 | ||||
| 382.214 | -91.51235199 | 0.000026 | -78.429338 | 0.000116 | ||||
| 387.597 | -90.398956299 | 0.000029 | -77.315942 | 0.000132 | ||||
| 392.98 | -89.876708984 | 0.000031 | -76.793694 | 0.000140 | ||||
| 398.364 | -90.923301697 | 0.000027 | -77.840287 | 0.000124 | ||||
| 403.747 | -91.519126892 | 0.000026 | -78.436112 | 0.000116 | ||||
| 409.13 | -89.880500793 | 0.000031 | -76.797486 | 0.000140 | ||||
| 414.514 | -88.523574829 | 0.000036 | -75.440560 | 0.000164 | ||||
| 419.897 | -88.133514404 | 0.000038 | -75.050500 | 0.000172 | ||||
| 425.28 | -88.516792297 | 0.000036 | -75.433778 | 0.000164 | ||||
| 430.664 | -89.156494141 | 0.000034 | -76.073480 | 0.000152 | ||||
| 436.047 | -87.890579224 | 0.000039 | -74.807565 | 0.000177 | ||||
| 441.43 | -85.652374268 | 0.000050 | -72.569360 | 0.000229 | ||||
| 446.813 | -84.840530395 | 0.000055 | -71.757516 | 0.000251 | ||||
| 452.197 | -85.262886047 | 0.000053 | -72.179872 | 0.000239 | ||||
| 457.58 | -83.171646118 | 0.000067 | -70.088632 | 0.000304 | ||||
| 462.963 | -81.689323425 | 0.000080 | -68.606309 | 0.000361 | ||||
| 468.347 | -82.263893127 | 0.000075 | -69.180879 | 0.000338 | ||||
| 473.73 | -82.18787384 | 0.000075 | -69.104859 | 0.000341 | ||||
| 479.113 | -81.208557129 | 0.000084 | -68.125543 | 0.000382 | ||||
| 484.497 | -80.67867279 | 0.000090 | -67.595658 | 0.000406 | ||||
| 489.88 | -79.529258728 | 0.000102 | -66.446244 | 0.000464 | ||||
| 495.263 | -77.378211975 | 0.000131 | -64.295197 | 0.000595 | ||||
| 500.646 | -75.369140625 | 0.000165 | -62.286126 | 0.000750 | ||||
| 506.03 | -68.718086243 | 0.000357 | -55.635072 | 0.001617 | ||||
| 511.413 | -48.354701996 | 0.003749 | -35.271688 | 0.016997 | 511.413 | 1.952 | ||
| 516.796 | -35.254192352 | 0.017031 | -22.171178 | 0.077203 | 516.796 | 1.973 | ||
| 522.18 | -29.914909363 | 0.031559 | -16.831895 | 0.143059 | 522.18 | 522.18 | 1.993 | |
| 527.563 | -31.24259758 | 0.027071 | -18.159583 | 0.122717 | 527.563 | 2.014 | ||
| 532.946 | -39.491184235 | 0.010439 | -26.408170 | 0.047321 | 532.946 | 2.034 | ||
| 538.33 | -55.822975159 | 0.001582 | -42.739961 | 0.007172 | 538.33 | 2.055 | ||
| 543.713 | -69.834373474 | 0.000314 | -56.751359 | 0.001421 | ||||
| 549.096 | -76.108032227 | 0.000152 | -63.025018 | 0.000689 | ||||
| 554.479 | -78.890701294 | 0.000110 | -65.807687 | 0.000499 | ||||
| 559.863 | -80.829551697 | 0.000088 | -67.746537 | 0.000399 | ||||
| 565.246 | -83.096923828 | 0.000068 | -70.013909 | 0.000307 | ||||
| 570.629 | -84.631317139 | 0.000057 | -71.548303 | 0.000257 | ||||
| 576.013 | -82.746414185 | 0.000071 | -69.663400 | 0.000320 | ||||
| 581.396 | -81.756958008 | 0.000079 | -68.673944 | 0.000359 | ||||
| 586.779 | -82.44758606 | 0.000073 | -69.364572 | 0.000331 | ||||
| 592.163 | -83.822471619 | 0.000062 | -70.739457 | 0.000282 | ||||
| 597.546 | -83.378852844 | 0.000066 | -70.295838 | 0.000297 | ||||
| 602.929 | -82.729164124 | 0.000071 | -69.646150 | 0.000320 | ||||
| 608.312 | -81.905899048 | 0.000078 | -68.822885 | 0.000352 | ||||
| 613.696 | -80.269325256 | 0.000094 | -67.186311 | 0.000426 | ||||
| 619.079 | -79.258300781 | 0.000106 | -66.175286 | 0.000478 | ||||
| 624.462 | -80.167129517 | 0.000095 | -67.084115 | 0.000431 | ||||
| 629.846 | -81.591705322 | 0.000081 | -68.508691 | 0.000365 | ||||
| 635.229 | -80.961410522 | 0.000087 | -67.878396 | 0.000393 | ||||
| 640.612 | -80.006202698 | 0.000097 | -66.923188 | 0.000439 | ||||
| 645.996 | -80.162658691 | 0.000095 | -67.079644 | 0.000431 | ||||
| 651.379 | -80.944152832 | 0.000087 | -67.861138 | 0.000394 | ||||
| 656.762 | -80.477416992 | 0.000092 | -67.394403 | 0.000416 | ||||
| 662.145 | -80.032951355 | 0.000097 | -66.949937 | 0.000438 | ||||
| 667.529 | -80.942932129 | 0.000087 | -67.859918 | 0.000394 | ||||
| 672.912 | -81.363418579 | 0.000083 | -68.280404 | 0.000375 | ||||
| 678.295 | -79.422325134 | 0.000104 | -66.339311 | 0.000470 | ||||
| 683.679 | -78.093536377 | 0.000121 | -65.010522 | 0.000547 | ||||
| 689.062 | -78.338142395 | 0.000117 | -65.255128 | 0.000532 | ||||
| 694.445 | -80.070396423 | 0.000096 | -66.987382 | 0.000436 | ||||
| 699.829 | -82.363945007 | 0.000074 | -69.280931 | 0.000334 | ||||
| 705.212 | -82.090003967 | 0.000076 | -69.006989 | 0.000345 | ||||
| 710.595 | -81.286468506 | 0.000084 | -68.203454 | 0.000379 | ||||
| 715.979 | -82.073379517 | 0.000076 | -68.990365 | 0.000346 | ||||
| 721.362 | -81.182632446 | 0.000085 | -68.099618 | 0.000383 | ||||
| 726.745 | -77.841552734 | 0.000124 | -64.758538 | 0.000564 | ||||
| 732.128 | -75.235069275 | 0.000168 | -62.152055 | 0.000762 | ||||
| 737.512 | -74.476959228 | 0.000183 | -61.393945 | 0.000831 | ||||
| 742.895 | -74.897628784 | 0.000175 | -61.814614 | 0.000792 | ||||
| 748.278 | -74.880226135 | 0.000175 | -61.797212 | 0.000793 | ||||
| 753.662 | -74.386329651 | 0.000185 | -61.303315 | 0.000840 | ||||
| 759.045 | -73.438278198 | 0.000207 | -60.355264 | 0.000937 | ||||
| 764.428 | -68.009727478 | 0.000387 | -54.926713 | 0.001755 | ||||
| 769.812 | -45.380805969 | 0.005287 | -32.297791 | 0.023964 | 769.812 | 2.938 | ||
| 775.195 | -25.856210709 | 0.050437 | -12.773196 | 0.228638 | 775.195 | 2.959 | ||
| 780.578 | -15.919221878 | 0.158967 | -2.836207 | 0.720614 | 780.578 | 2.979 | ||
| 785.961 | -13.083014488 | 0.220599 | 0.000000 | 1.000000 | 785.961 | 785.961 | 3.000 | |
| 791.345 | -16.786815643 | 0.143806 | -3.703801 | 0.651890 | 791.345 | 3.020 | ||
| 796.728 | -27.805599213 | 0.040267 | -14.722585 | 0.182534 | 796.728 | 3.041 | ||
| 802.111 | -48.840049744 | 0.003545 | -35.757035 | 0.016070 | 802.111 | 3.061 | ||
| 807.495 | -64.689453125 | 0.000568 | -51.606439 | 0.002575 | 807.495 | 3.082 | ||
| 812.878 | -68.400802612 | 0.000370 | -55.317788 | 0.001677 | ||||
| 818.261 | -70.800331116 | 0.000280 | -57.717317 | 0.001271 | ||||
| 823.645 | -72.878097534 | 0.000221 | -59.795083 | 0.001000 | ||||
| 829.028 | -72.702392578 | 0.000225 | -59.619378 | 0.001020 | ||||
| 834.411 | -72.308296204 | 0.000236 | -59.225282 | 0.001068 | ||||
| 839.794 | -73.016204834 | 0.000217 | -59.933190 | 0.000984 | ||||
| 845.178 | -73.797607422 | 0.000198 | -60.714593 | 0.000899 | ||||
| 850.561 | -74.792755127 | 0.000177 | -61.709741 | 0.000802 | ||||
| 855.944 | -75.17313385 | 0.000169 | -62.090119 | 0.000767 | ||||
| 861.328 | -74.636276245 | 0.000180 | -61.553262 | 0.000816 | ||||
| 866.711 | -75.881858826 | 0.000156 | -62.798844 | 0.000707 | ||||
| 872.094 | -77.047775269 | 0.000136 | -63.964761 | 0.000618 | ||||
| 877.478 | -76.190200806 | 0.000150 | -63.107186 | 0.000682 | ||||
| 882.861 | -76.280487061 | 0.000149 | -63.197473 | 0.000675 | ||||
| 888.244 | -77.665000915 | 0.000127 | -64.581986 | 0.000575 | ||||
| 893.627 | -79.851875305 | 0.000099 | -66.768861 | 0.000447 | ||||
| 899.011 | -81.405792236 | 0.000082 | -68.322778 | 0.000373 | ||||
| 904.394 | -81.163497925 | 0.000085 | -68.080483 | 0.000384 | ||||
| 909.777 | -81.698272705 | 0.000080 | -68.615258 | 0.000361 | ||||
| 915.161 | -83.446800232 | 0.000065 | -70.363786 | 0.000295 | ||||
| 920.544 | -83.188690186 | 0.000067 | -70.105676 | 0.000304 | ||||
| 925.927 | -80.394920349 | 0.000093 | -67.311906 | 0.000420 | ||||
| 931.311 | -78.437446594 | 0.000116 | -65.354432 | 0.000526 | ||||
| 936.694 | -78.010147095 | 0.000122 | -64.927133 | 0.000553 | ||||
| 942.077 | -78.544929504 | 0.000115 | -65.461915 | 0.000520 | ||||
| 947.46 | -77.550468445 | 0.000129 | -64.467454 | 0.000583 | ||||
| 952.844 | -76.339370728 | 0.000148 | -63.256356 | 0.000670 | ||||
| 958.227 | -73.449790955 | 0.000206 | -60.366776 | 0.000936 | ||||
| 963.61 | -71.536727905 | 0.000258 | -58.453713 | 0.001168 | ||||
| 968.994 | -71.562828064 | 0.000257 | -58.479814 | 0.001164 | ||||
| 974.377 | -71.906173706 | 0.000247 | -58.823159 | 0.001119 | ||||
| 979.76 | -72.119720459 | 0.000241 | -59.036706 | 0.001092 | ||||
| 985.144 | -72.184005737 | 0.000239 | -59.100991 | 0.001083 | ||||
| 990.527 | -70.800994873 | 0.000280 | -57.717980 | 0.001271 | ||||
| 995.91 | -69.533454895 | 0.000325 | -56.450440 | 0.001472 | ||||
| 1001.293 | -69.560585022 | 0.000324 | -56.477571 | 0.001467 | ||||
| 1006.677 | -70.700141907 | 0.000284 | -57.617127 | 0.001286 | ||||
| 1012.06 | -69.322128296 | 0.000333 | -56.239114 | 0.001508 | ||||
| 1017.443 | -66.92073822 | 0.000439 | -53.837724 | 0.001990 | ||||
| 1022.827 | -65.707038879 | 0.000505 | -52.624024 | 0.002290 | ||||
| 1028.21 | -62.275829315 | 0.000751 | -49.192815 | 0.003403 | 1028.21 | 3.924 | ||
| 1033.593 | -42.277099609 | 0.007566 | -29.194085 | 0.034299 | 1033.593 | 3.945 | ||
| 1038.977 | -26.936546326 | 0.044519 | -13.853532 | 0.201811 | 1038.977 | 3.966 | ||
| 1044.36 | -19.652082443 | 0.103281 | -6.569068 | 0.468187 | 1044.36 | 3.986 | ||
| 1049.743 | -19.015262604 | 0.111166 | -5.932248 | 0.503929 | 1049.743 | 1049.743 | 4.007 | |
| 1055.126 | -24.944141388 | 0.056042 | -11.861127 | 0.254043 | 1055.126 | 4.027 | ||
| 1060.51 | -38.655513763 | 0.011497 | -25.572499 | 0.052118 | 1060.51 | 4.048 | ||
| 1065.893 | -59.193031311 | 0.001072 | -46.110017 | 0.004859 | 1065.893 | 4.068 | ||
| 1071.276 | -67.643638611 | 0.000404 | -54.560624 | 0.001831 |
L'originale continua per un totale di 4096 righe. Queste sono le spiegazioni (il numero è quello della colonna da sin. a des.).
 La cosa curiosa è che, secondo il foglio elettronico, i calcoli dicono che la fondamentale dovrebbe essere vicina a 263.7 mentre tutte le armoniche sono basate all'incirca su 262. Comunque 1.7 Hz non fa una grande differenza ed è inferiore alla JND che, a questa frequenza è ≈3.4 Hz, quindi la differenza non è nemmeno percepibile. Inoltre ricordiamo che, negli strumenti, piccole differenze di frequenza (sempre ≤ JND) rispetto ai valori teorici sia per la fondamentale che per le componenti, sono normali. Una differenza in frequenza così piccola è sopportabile anche perché, in questo caso, noi sappiamo già che il suono ha componenti armoniche e quello che ci interessa non sono le loro frequenze, ma le loro ampiezze.
La cosa curiosa è che, secondo il foglio elettronico, i calcoli dicono che la fondamentale dovrebbe essere vicina a 263.7 mentre tutte le armoniche sono basate all'incirca su 262. Comunque 1.7 Hz non fa una grande differenza ed è inferiore alla JND che, a questa frequenza è ≈3.4 Hz, quindi la differenza non è nemmeno percepibile. Inoltre ricordiamo che, negli strumenti, piccole differenze di frequenza (sempre ≤ JND) rispetto ai valori teorici sia per la fondamentale che per le componenti, sono normali. Una differenza in frequenza così piccola è sopportabile anche perché, in questo caso, noi sappiamo già che il suono ha componenti armoniche e quello che ci interessa non sono le loro frequenze, ma le loro ampiezze.
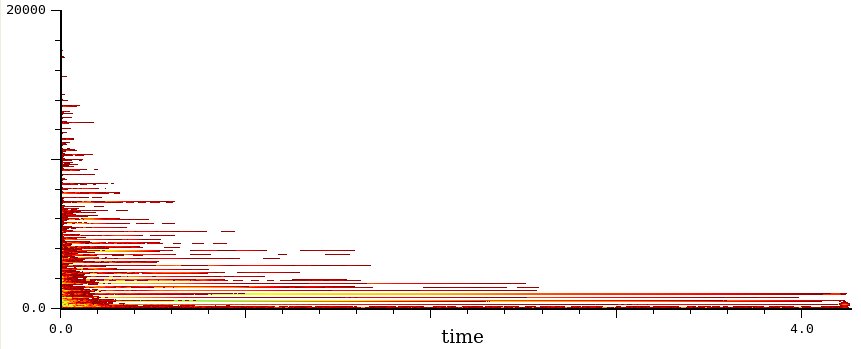
Comunque, grazie a Ceres3, che esporta anche i dati del sonogramma in un blocco da 1280808 righe, ho creato il grafico a destra che mostra come varia la frequenza della fondamentale nel corso del sustain (esclusi attacco e decay in cui varia molto di più). Come vedete cambia parecchio, ma resta sempre in un range di poco più di 1 Hz, quindi, anche qui, non percepibile, se escludiamo il picco iniziale e quello finale. La linea rossa è la media.
Alla fine, ecco i grafici delle componenti selezionate con la loro ampiezza. Con questi dati è stata realizzata la risintesi che avete ascoltato sopra.
 |
 |
Ora un altro problema è: se la FFT è istantanea e anche selezionando tutto il segnale si ottiene solo uno spettro che rappresenta una media, come si può creare una mappa completa dell'evoluzione di un suono nel tempo?
La risposta, in teoria, è semplice: per poter ottene una tale mappa, occorre fare una serie di singole analisi a intervalli regolari per tutta la durata dell'evento sonoro e questa volta non fare la media, ma disporre tutte le ampiezza delle bande una accanto altra come se fossero i fotogrammi di un video. Otteniamo così un sonogramma in cui abbiamo il tempo sull'asse X, le frequenze sull'asse Y e ogni banda è rappresentata da una linea che si estende nel tempo, il cui colore è tanto più contrastato rispetto allo sfondo quanto è maggiore l'ampiezza.
Poiché la rappresentazione è sul piano e le dimensioni da rappresentare sono 3 (frequenze, ampiezza e tempo), per l'ampiezza si ricorre al colore. Lo schema dei colori può essere diverso, ma l'importante è che sia in grado di evidenziare le differenze di ampiezza creando con lo sfondo un contrasto tanto maggiore quanto più l'ampiezza è elevata. Questo e il sonogramma del suono di oboe analizzato poco fa.
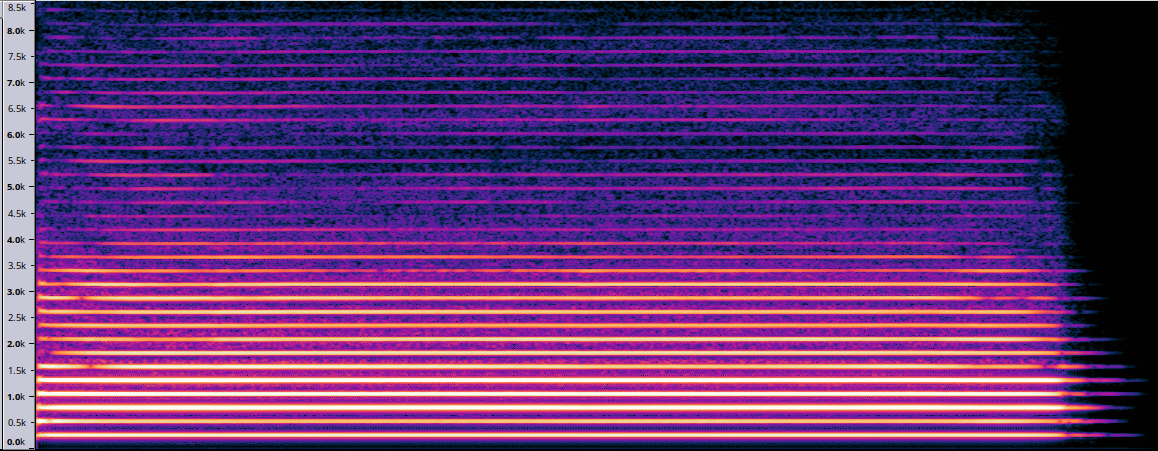
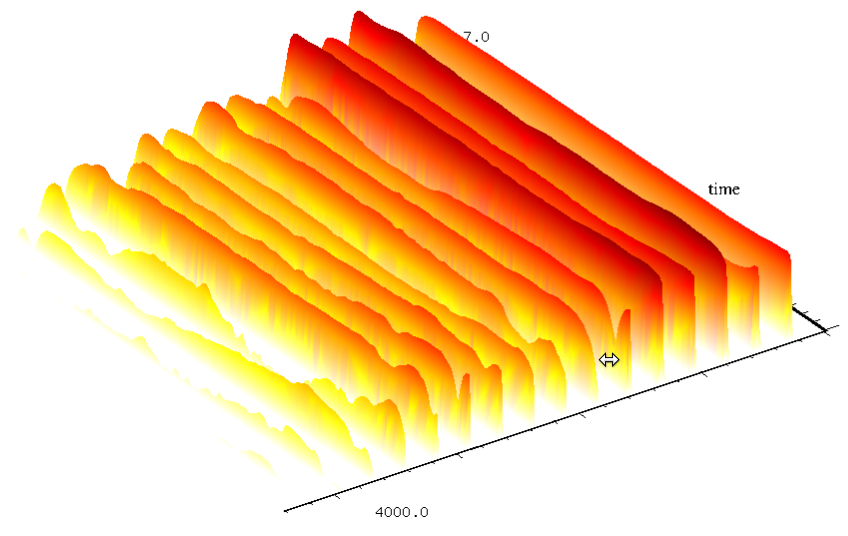
Con lo stesso procedimento si può ottenere uno spettrogramma. Si tratta di una rappresentazione 3D in cui abbiamo ancora le frequenze sull'asse X, il tempo sull'asse Y, mentre le ampiezze sono rappresentate come altezze sull'asse Z. In tal modo è possibile distinguere chiaramente anche l'inviluppo dei singoli armonici. Ovviamente in quest'ultimo caso la colorazione è accessoria e non del tutto necessaria, però. se è sensata, aiuta, così come aiuta il fatto che lo spettrogramma possa essere ruotato e studiato da diverse prospettive.
Fra l'altro osservate come questo spettrogramma 3D permetta di notare che non tutte le componenti abbiano un attacco sfz, soltanto alcune. Si tratta di una cosa che era impossibile osservare con qualsiasi altra rappresentazione perché ci vuole qualcosa che ci permetta di vedere gli inviluppi delle singole componenti. Il software che utilizzo si chiama "snd" ed è stato scritto da Bill Schottstaedt del CCRMA (si legge "karma") all'Università di Stanford all'inizio degli anni 80, quando ancora il mouse non esisteva, per un computer PDP-10 e portato su Linux in anni più recenti. Tutti gli spettrogrammi-3D che ho pubblicato (e anche molti sonogrammi e spettri) sono prodotti da questo software.
Nel caso del sonogramma, dobbiamo anche tener conto della velocità con cui il suono cambia nel tempo. I suoni emessi dagli strumenti musicali variano abbastanza lentamente e con una certa gradualità, tranne che nel momento dell'attacco in cui possono esserci anche variazioni molto veloci (i cosiddetti "transitori" o "transienti").
In natura, però, possiamo trovare anche suoni che, nel corso della loro vita, esibiscono variazioni molto complesse e veloci. In tal caso, a volte, la ricerca di una maggiore risoluzione in frequenza, aumentando il numero dei punti e quindi la lunghezza del segmento su cui si fa l'analisi, può contrastare con la visione di variazioni temporali troppo veloci. La risoluzione in frequenza contrasta con la risoluzione temporale.
Ragioniamo: se ho un suono campionato a 44100 e la mia finestra di analisi è lunga 16384 punti, essa dura 16384 / 44100 = 0.37 secondi, il che significa che ogni variazione che dura meno ha buone probabilità di risultare malamente definita in senso temporale. La cosa è mitigata solo dal fatto che, nella serie di analisi per creare il sonogramma, le finestre delle varie analisi vengono parzialmente sovrapposte. Comunque, in questi casi, una FFT con pochi punti seguirà meglio il fenomeno rispetto a una con più punti, anche se quest'ultima produce risultati più definiti in frequenza.
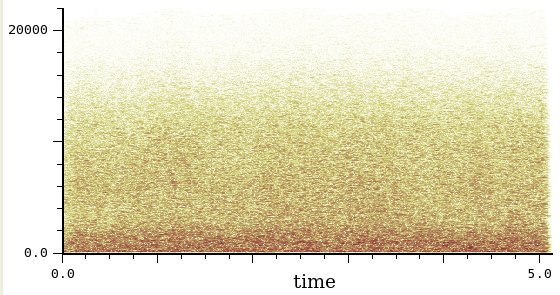
Ascoltate questo uccellino e osservate il sonogramma nella figura qui sotto. Fatelo varie volte in modo da capire bene la corrispondenza fra suono e rappresentazione.
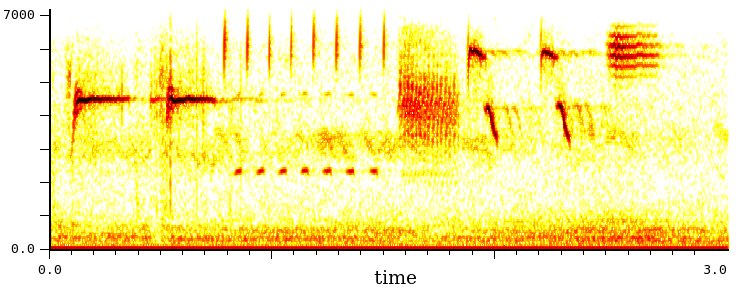
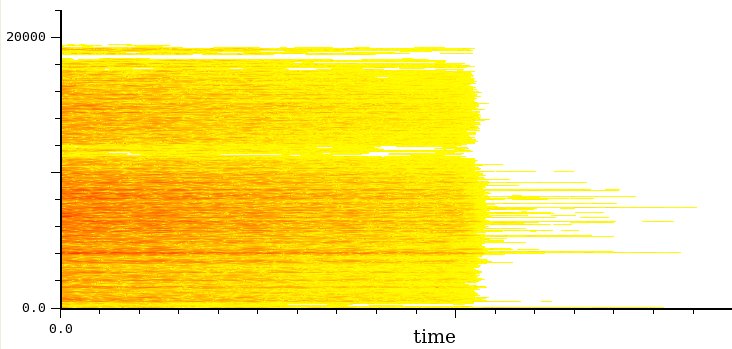
Il numero di punti di questo sonogramma è 1024. Supponiamo di voler aumentare la risoluzione in frequenza e aumentiamo il numero di punti a 16384. Quello che otteniamo è il sonogramma seguente
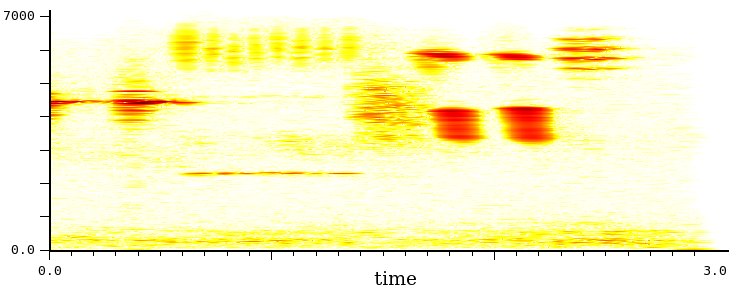
Notate come le variazioni rapide siano andate quasi completamente perse. In particolare, non si vedono più i veloci glissati discendenti a circa 2 sec., il cui posto è stato preso da due masse la cui estensione va dalla frequenza superiore a quella inferiore dell'intero glissato.
Nel caso dei sonogrammi, quindi, è molto importante scegliere il giusto numero di punti cercando un compromesso fra definizione in frequenza e definizione temporale.
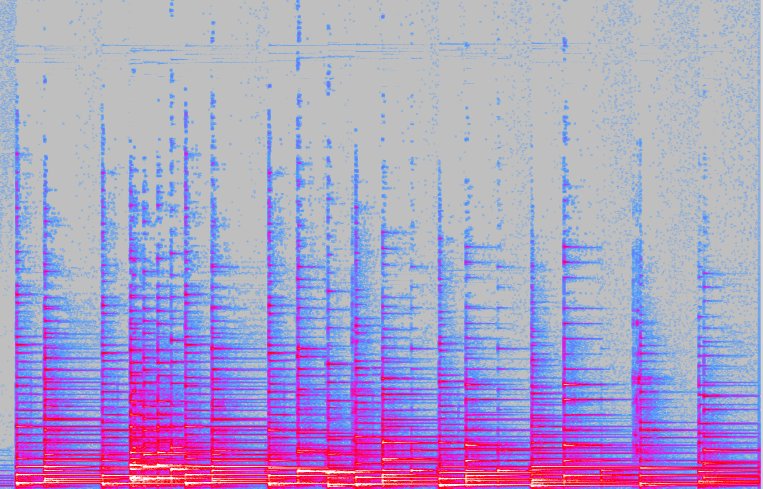
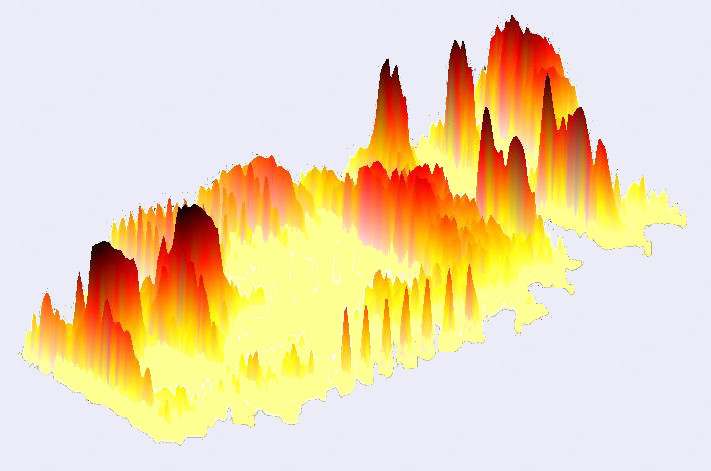
Curiosità finale: guardate il paesaggio disegnato dallo spettrogramma-3D del canto dell'uccellino.
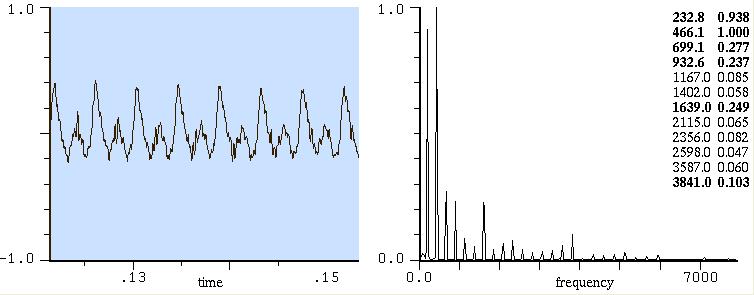
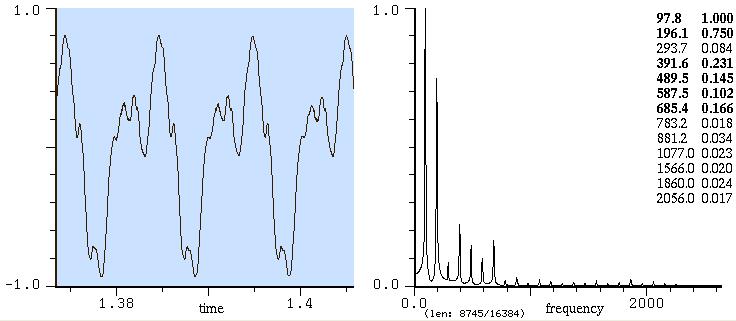
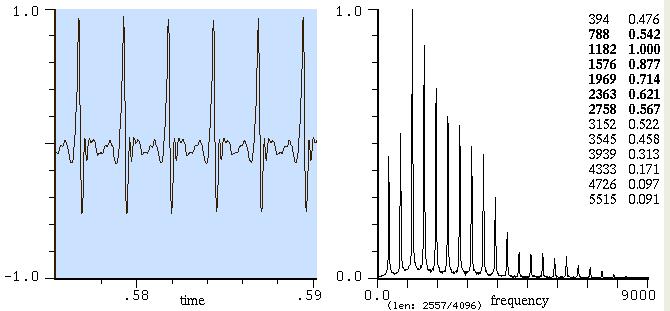
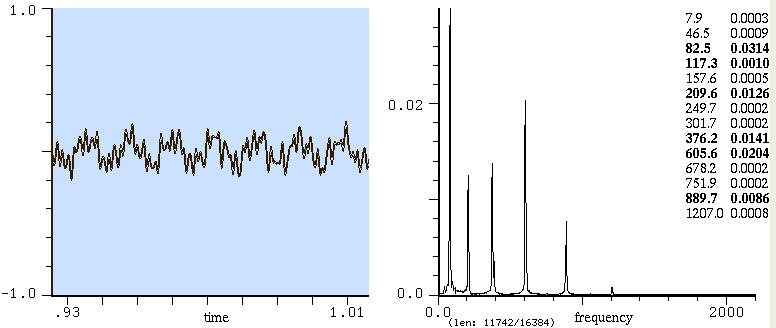
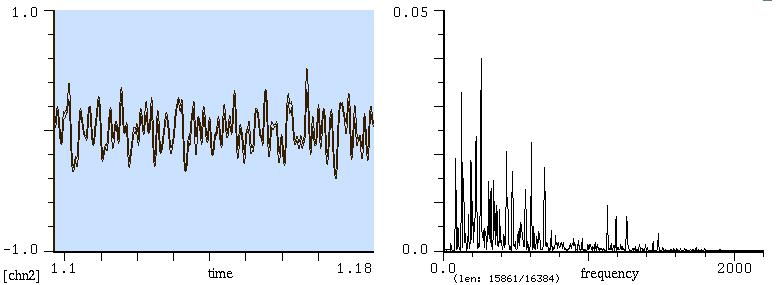
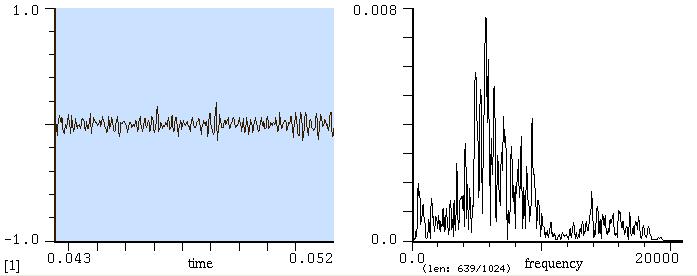
Sib di pianoforte
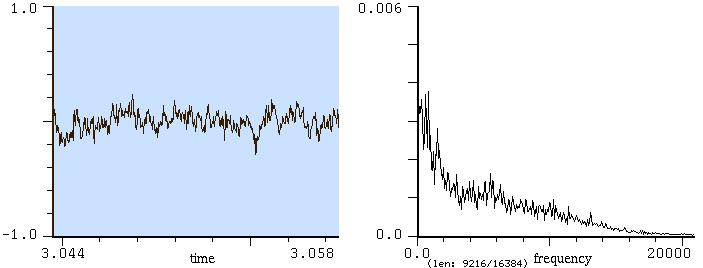
Sol basso di violoncello
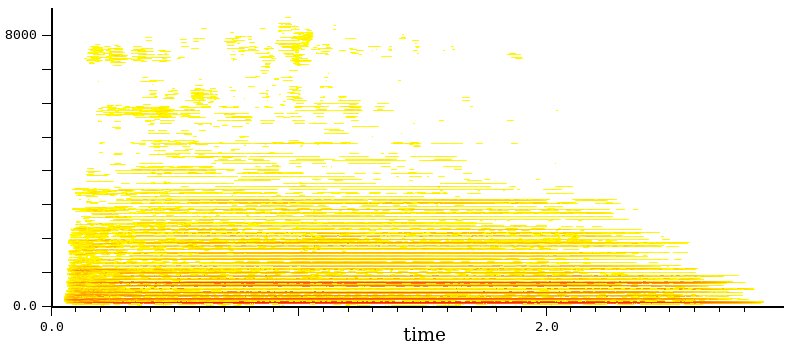
Sol di tromba
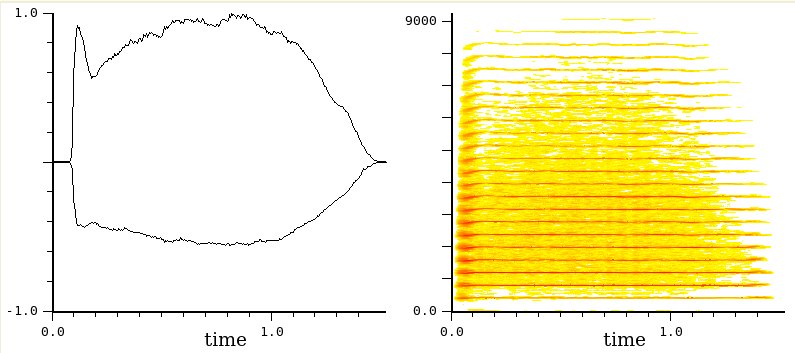
Gong
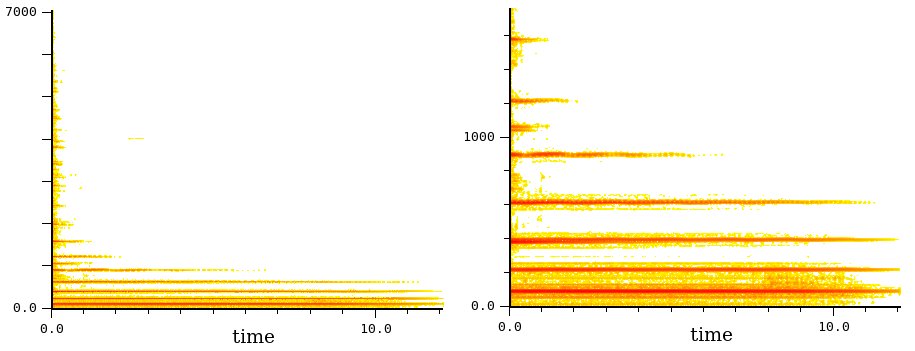
Tamtam
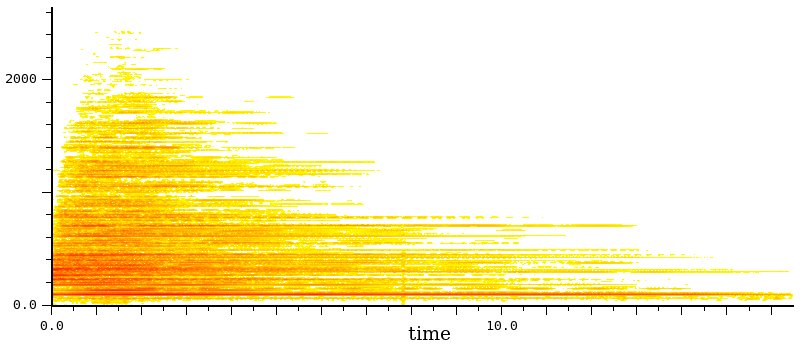
Piatto
Fontana