Mauro Graziani
Tecniche di Sintesi
L'oscillatore digitale
Prima di partire con la descrizione delle tecniche di sintesi vere e
proprie, sarà utile chiarire, sia pure in breve, i principi di
funzionamento di uno dei moduli maggiormente utilizzati in questo
campo: l'oscillatore digitale.
In realtà si possono capire le tecniche di sintesi anche senza
sapere esattamente come funziona un oscillatore digitale, assumendo
fideisticamente il fatto che questo modulo è in grado di riprodurre
correttamente qualsiasi forma d'onda periodica, ma la conoscenza non
è mai inutile e in questo caso specifico mette in luce alcuni
aspetti della tecnologia digitale, che spesso non è così precisa
come si pensa.
NB: quello descritto qui è il classico "wavetable oscillator", cioè
l'oscillatore basato su tabella che si trova in varie forma in
Csound (oscil, oscili, oscil3, etc) e in Max/MSP (cycle~).
Descrizione
L'oscillatore digitale è un dispositivo software che legge
ciclicamente una tabella numerica in cui è memorizzato un ciclo
della forma d'onda da produrre. La lettura avviene mediante un
incremento di fase che è calcolato in base alla frequenza da
produrre e alla frequenza di campionamento.
Se, per fare un esempio, si desidera produrre una sinusoide a 440
Hz, occorre, prima di tutto, memorizzare in tabella un ciclo della
forma d'onda richiesta (in questo caso, una sinusoide) e poi far
partire un oscillatore indirizzandolo alla tabella suddetta e
specificando la frequenza desiderata.
L'oscillatore scandirà l'intera tabella in 1/440 di secondo,
procedendo ciclicamente (cioè dall'inizio alla fine e poi da capo),
generando, in questo modo, un'onda sinusoidale avente un periodo
pari alla frequenza richiesta.
Ecco uno schema:
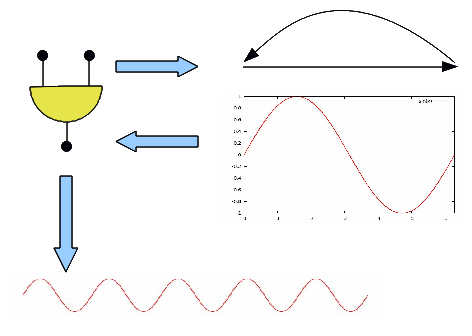
Il dettaglio è semplice, ma non del tutto banale.
La tabella
Innanzitutto, con il termine tabella (detta anche array
unidimensionale o vettore) si intende una struttura
dati formata da una serie di locazioni di memoria consecutive. Per
accedere ai singoli valori, quindi, basta conoscere la locazione di
partenza e sommare un numero indice che rappresenta la posizione
dell'elemento desiderato.
Supponendo che la tabella si chiami T, l'ennesimo valore sarà
indicato con Tn o scritture equivalenti (T[n], T(n),
etc). In pratica, supponendo che la tabella sia memorizzata a
partire dalla locazione 1000, il primo valore si troverà alla
locazione 1000, il secondo alla locazione 1001, il terzo alla 1002,
... ,l'ennesimo alla locazione (T + n - 1). Si noti, però, che, per
convenzione, in alcuni linguaggi di programmazione (e.g. C, Phyton e
altri) il primo valore è definito come di indice 0 (zero: T0,
quindi il valore con indice n si troverà alla locazione T + n),
mentre in altri (Pascal e altri) ha indice 1 (T1, quindi
il valore con indice n si troverà alla locazione T + n - 1).
Lunghezza della tabella
Nei linguaggi di sintesi, comunque, questo meccanismo di lettura è
trasparente all'utente che non se ne deve preoccupare, se non per un
particolare: la lunghezza della tabella. Di solito, infatti, si
richiede una lunghezza multipla di 2 (128, 256, 512, 1024, 2048,
4096, 8192, etc).
Anche il lettore ingenuo può intuire che questa imposizione è
collegata alla particolare numerazione utilizzata dal computer, che
codifica i numeri in base 2. In dettaglio, una lunghezza pari a una
potenza di 2 consente alla macchina di risparmiare un test,
velocizzando il processo di lettura. Una lettura ciclica, infatti,
prevede che, una volta superata l'ultima locazione, si ritorni alla
prima. Per farlo, è necessario testare il valore dell'indice prima
di ogni lettura con un codice tipo
if (index >= lunghezza_tabella) then index = index -
lunghezza_tabella
oppure eseguire l'operazione di modulo
index = index mod lunghezza_tabella
Sia il test che il modulo, eseguiti SR volte al secondo (SR =
frequenza di campionamento, e.g. 44100), consumano tempo che può
essere risparmiato con un semplice AND: posto che si sia
precalcolato il valore
lunghezza_tabella_meno_uno = lunghezza_tabella - 1
allora basta porre
index = index AND lunghezza_tabella_meno_uno
effettuando una operazione molto più veloce rispetto ai metodi di
cui sopra. Questo artificio, però, è possibile se e solo se la
lunghezza della tabella è una potenza di 2 perché solo in questo
caso il valore lunghezza_tabella_meno_uno, in binario, è una serie
ininterrotta di 1 che, con l'operazione di AND, elimina tutte le
cifre superiori.
Esempio: sia lunghezza_tabella = 256 = 28, in binario
0000000100000000, allora lunghezza_tabella_meno_uno = 255, in
binario 0000000011111111. Ora, finché l'indice è <= 255, l'AND
con 255 lo lascia inalterato, ma quando l'indice è > 255,
l'effetto dell'AND è quello di azzerare tutte le cifre superiori,
riportando l'indice nell'ambito richiesto con il minimo consumo di
tempo di calcolo.
Importanza della lunghezza della tabella
Alcuni sistemi, come Csound, lasciano all'utente l'onere di
scegliere la lunghezza della tabella in cui memorizzare la forma
d'onda. La scelta non è banale perché può influire sulla definizione
della forma d'onda. Se quest'ultima è insufficiente si produrranno
approssimazioni con un rumore di quantizzazione sensibile.
Il perché è semplice. Supponiamo che si voglia memorizzare in
tabella una sinusoide, senza armonici. La tabella sarà riempita con
valori di sin(x), con x che va da 0 a 2π (un ciclo) in
un numero di passi pari alla lunghezza della tabella.
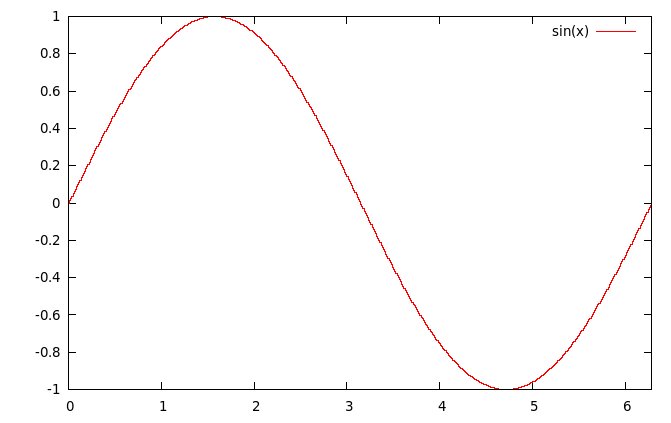
Nel digitale, la funzione non è mai continua, ma approssimata con
una serie di gradini. Ne consegue che la definizione della curva
memorizzata è direttamente proporzionale alla dimensione della
tabella.
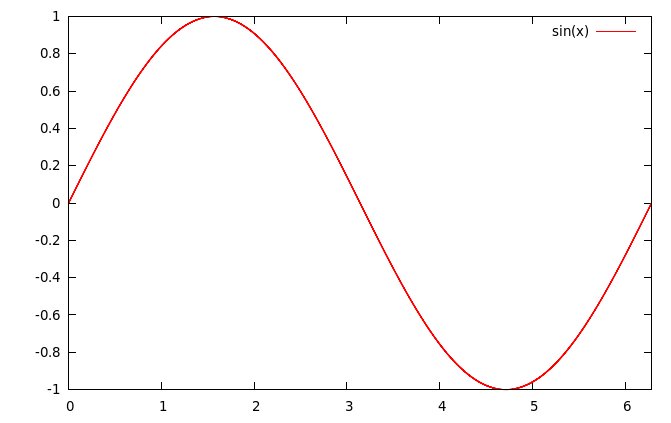
A titolo di esempio, ecco come appare una sinusoide calcolata con
16, 128, 512 e 4096 punti. La differenza si vede già così, ma
cliccando su una qualsiasi immagine si aprirà una pagina con
ingrandimenti in cui si vede che anche la funzione calcolata in 512
punti è lungi dall'essere buona (ovviamente 16 punti è un caso
assurdo, ma rende l'idea; per tornare qui usate il link "Back" a
fine pagina). Per informazione, in Csound ver. 5.00 la massima
lunghezza della tabella è 16777216 (224).
Abbiamo, quindi, un primo dato di fatto: la risoluzione della forma
d'onda è proporzionale alla lunghezza della tabella. Tutto ciò può
avere un impatto non banale sulla qualità dell'audio generato
dall'oscillatore, come vedremo.
Il meccanismo di lettura
Poco fa, nella descrizione, abbiamo detto che, per ottenere 440 Hz,
"l'oscillatore scandirà l'intera tabella in 1/440 di secondo,
procedendo ciclicamente". Concettualmente è vero, ma praticamente i
programmi di sintesi non si comportano così. In un software come
Csound o Max/MSP, il tempo non ha alcuna importanza e non viene
minimamente considerato come tale. L'unico parametro collegato al
tempo che questi software maneggiano, infatti, è il numero di
campioni audio calcolato in base alla frequenza di campionamento
(SR).
Se, per esempio, dite a Csound di generare un suono per 2 secondi,
questo valore temporale sarà immediatamente trasformato in campioni
moltiplicandolo per SR e il software scriverà nel file di uscita SR
* 2 campioni per ogni canale 1. SR, in pratica, viene ad essere l'unica unità
di misura del tempo e lo spazio di un campione è il più piccolo
intervallo esistente (il "quantum" temporale) 2. Ma, attenzione: la definizione di quantum
temporale non è un colorito modo di dire, perché, proprio come
nell'analoga teoria fisica, il quantum non è solo l'intervallo
minimo, ma anche il sottomultiplo, base di tutti gli intervalli
temporali. In pratica, non esiste, in digitale, un intervallo
temporale pari a 1.5 campioni (e in genere a n.k campioni).
Esistono solo intervalli temporali pari a un numero
intero di campioni.
Quindi, quando dite a Csound (o Max/MSP) SR = 44100, stabilite anche
altre due cose:
- il minimo intervallo temporale che il software può concepire,
pari a 1/SR (per Max/MSP vedi 3)
- la scala dei tempi che è formata da multipli di 1/SR
È importante capire che il software procede nel tempo a passi di
1/SR, quindi esistono i tempi 1/SR, 2/SR, 3/SR, ma non c'è niente
fra loro; il tempo 1.5/SR semplicemente non esiste: la scala dei
tempi è discreta (a gradini), non continua.
Per esempio, se SR = 44100, allora 1/SR = 0.0000226757369615
secondi. Quindi il procedere del tempo in secondi è:
0 - 0.0000226757369615 - 0.000045351473923 - 0.0000680272108845 -
...
Qualsiasi intervallo fra questi, per es. 0.00005, non esiste
proprio. Ne consegue che, se chiedete a Csound di fare un suono che
parte all'istante 0 e termina all'istante 1.00005 (con SR = 44100),
per il software sarà impossibile farlo. O termina a
1.000045351473923, o termina a 1.0000680272108845. La risoluzione
temporale è 1/SR.
Così, a differenza dell'analogico in cui, almeno nella comune
immagine mentale, si passa, senza soluzione di continuità,
attraverso tutti i valori possibili, nel digitale non è così. Nello
stesso modo, nell'analogico esiste sempre un ε (epsilon) piccolo a
piacere che fa sì che il campo dei numeri reali (numeri con virgola)
sia continuo (dati due numeri qualsiasi A e B, con A < B, si può
sempre trovare un numero che sta in mezzo: A < K < B), mentre
nel digitale a un certo punto ci si deve fermare (se non erro,
l'aritmetica floating point a 32 bit, nel caso migliore, si ferma al
18° decimale).
Una conseguenza di tutto ciò è che il digitale è sempre
approssimato, cioè contiene una certa quantità di rumore. Non si
esaltino i sostenitori dell'analogico, perché il rumore del digitale
può essere ridotto a livelli infinitamente inferiori rispetto a
quello presente nei circuiti analogici. In realtà, la continuità
dell'analogico è un'astrazione e mi fa pensare sempre al punto
euclideo che non ha dimensioni.
Qui, però, non voglio nemmeno iniziare una discussione su pregi e
difetti dei due sistemi. Tutto questo discorso è qui solo per
introdurre l'idea di approssimazione del digitale.
Abbiamo già visto, infatti, come, in dipendenza dalla lunghezza
della tabella, la forma d'onda venga calcolata in un numero finito
di passi e questa è già una prima approssimazione. Anche se
l'oscillatore leggesse tutti i valori della tabella, il risultato
sarebbe approssimato.
Ma l'oscillatore non può leggere tutti i valori perché, per
rispettare la frequenza richiesta, deve generare ogni ciclo in un
tempo ben determinato. Per esempio, per ottenere un'onda a 100 Hz,
ogni ciclo deve durare 1/100 secondi = 0.01 secondi (il periodo è
l'inverso della frequenza).
Ora, dato che, come abbiamo accennato, i tempi devono essere
trasformati in numero di campioni, supponendo un SR tipico = 44100,
ogni ciclo della nostra forma d'onda sarà formato da 44100/100 = 441
campioni. Se l'SR fosse 48000, ogni ciclo avrebbe 480 campioni.
A questo punto, come può, l'oscillatore riprodurre un ciclo in 441 o
480 campioni se in tabella un ciclo è memorizzato con un numero di
campioni diverso? (512, 1024, o altra potenza di 2). E in generale,
come si può creare un ciclo in K campioni, diverso da quello con cui
è stato memorizzato in tabella?
La risposta è semplice e introduce una approssimazione ulteriore:
l'oscillatore non legge tutti i valori della tabella, ma la
scandisce saltando o doppiando alcuni valori. In pratica, calcola un
passo di incremento (SI = sampling increment) che gli permette di
scandire la tabella nel numero di campioni richiesto.
Un esempio per chiarire. Sia
- frequenza di campionamento (SR) = 44100
- lunghezza tabella (TL) = 1024
- frequenza richiesta (F) = 100 Hz
Con questi valori abbiamo un ciclo che consta di 441 campioni
(SR/F). Di conseguenza la tabella dovrà essere letta con un passo di
incremento SI = TL/441 = 1024/441 = 2.32199546485.
Quindi l'oscillatore leggerà dapprima il valore che si trova nella
posizione 0 della tabella, poi quelli che si trovano nelle posizioni
2.32199546485, 4.6439909297, 6.96598639455, 9.2879818594, ... etc,
incrementando sempre di 2.32199546485.
In questo modo l'oscillatore è in grado di scandire l'intera tabella
(un ciclo) in 441 campioni generando un'onda il cui periodo è 1/100
di secondo, cioè 100 Hz.
In generale, quindi, la formula per calcolare SI a partire da SR, TL
e F è SI = TL/(SR/F) = TL * F / SR.
Infatti, con i numeri di cui sopra si ottiene il valore
precedentemente calcolato: 1024 * 100 / 44100 = 2.32199546485.
Ovviamente, così facendo, si introduce un ulteriore grado di
imprecisione perché saltando da un valore a un altro della tabella
si creano gradini ancora più grandi di quelli che si avrebbero
leggendo tutti i valori in successione. A parità di lunghezza della
tabella, questa imprecisione aumenta via via che la frequenza
aumenta. Tenendo fissi i valori di SR e TL di cui sopra e cambiando
solo F, si vede che, se a 100 Hz si saltano 2.32199546485 campioni a
ogni passo, a 400 Hz SI diventa 9.28798185941, a 800 Hz è
18.5759637188, eccetera. Ma la cosa assume proporzioni notevoli con
frequenze molto alte: per es., a 5000 Hz, SI è 116.099773243, a
15000 Hz diventa 348.299319728 a e 20000 Hz (vicino alla frequenza
di Nyquist) SI è 464.399092971. Praticamente, a questa frequenza, ci
sono solo due campioni per ogni ciclo.
Nel migliore dei casi, a frequenze molto alte, più che una
sinusoide, si genera una triangolare. Fortunatamente quello che si
crea non è rumore, ma distorsione armonica con il primo armonico ben
oltre la frequenza di Nyquist, così il tutto viene tagliato dal
filtro sul DAC.
In effetti, una delle caratteristiche interessanti del wavetable
oscillator è che il segnale è, per forza di cose, periodico:
leggendo ciclicamente una tabella, anche riempita di numeri a caso,
si crea forzatamente un ciclo. Di conseguenza, con un solo
oscillatore tabellare è praticamente impossibile creare del rumore
vero e proprio (non periodico), se non per cause esterne
(imperfezioni nelle apparecchiature che generano per es. jitter).
Come vedremo, dal punto di vista delle tecniche di sintesi, questa
caratteristica è, nello stesso tempo, un vantaggio e un handicap.
Ora, però, dobbiamo affrontare un secondo scoglio. Un effetto del
Sampling Increment è che all'oscillatore, spesso, è richiesta la
lettura in tabella di campioni che non si trovano in posizioni
intere. Per esempio, nel caso di cui sopra, con SI = 2.32199546485,
l'oscillatore dovrebbe partire leggendo il valore che si trova nella
posizione 0 della tabella, poi quelli che si trovano nelle posizioni
2.32199546485, 4.6439909297, 6.96598639455, 9.2879818594, ... etc,
incrementando sempre di 2.32199546485.
Il problema è che non può farlo perché la tabella ha solo posizioni
intere (0, 1, 2, 3, ...). Per risolvere questo problema,
l'oscillatore può adottare varie tecniche, ognuna delle quali
produce una diversa quantità di errore e richiede differenti tempi
di calcolo o quantità di memoria. In generale i due sono legati da
una relazione inversa: più errore = meno calcolo/memoria, meno
errore = più calcoli/memoria.
Oscillatore a troncamento
Si tratta del sistema più semplice e più veloce, utilizzato, per
es., dal modulo oscil di Csound.
La parte frazionaria è, semplicemente, ignorata. Sia che si debba
leggere il campione 2.1 o 2.99, l'oscillatore va a leggere il
campione 2. La posizione di lettura in tabella è
int(fase_istantanea)
Questo sistema produce un errore pari, al massimo, alla più grande
differenza che esiste fra un campione e il successivo. A sua volta,
questo valore non è fisso, ma dipende dalla forma dell'onda e dalla
posizione nel ciclo (fase istantanea).
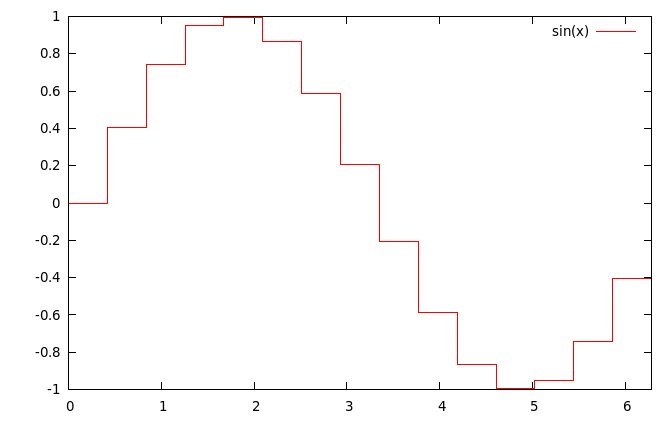
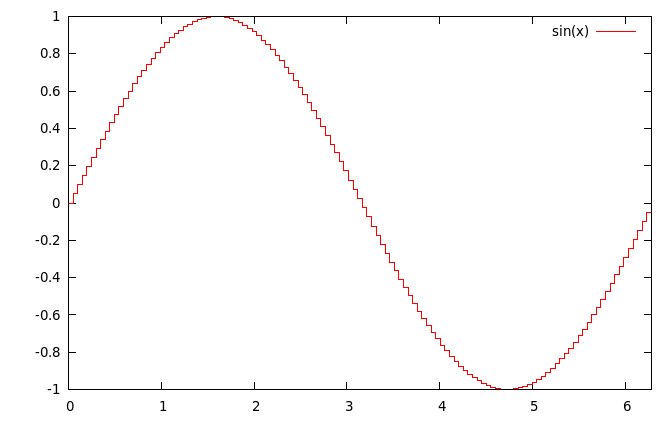 Guardando
la
figura
a
lato,
relativa
a
una
semplice
sinusoide
campionata
in
128
passi,
si
vede a occhio nudo come la differenza fra un campione e il
successivo non sia sempre uguale, ma aumenti dove la funzione ha
pendenza maggiore (ovvero, dove i gradini sono più alti) 4.
Guardando
la
figura
a
lato,
relativa
a
una
semplice
sinusoide
campionata
in
128
passi,
si
vede a occhio nudo come la differenza fra un campione e il
successivo non sia sempre uguale, ma aumenti dove la funzione ha
pendenza maggiore (ovvero, dove i gradini sono più alti) 4.
Qui l'importanza della lunghezza della tabella è massima. Più lunga
è la tabella, infatti, minore è il passo fra un campione e il
successivo. Di conseguenza, anche lo scarto fra i valori e quindi il
possibile errore, diminuisce.
Nella figura seguente (sotto) potete vedere un sonogramma che
contiene, l'uno dopo l'altro, sette suoni, visibili nella parte
superiore.
Tutti i suoni dovrebbero essere identici e contenere soltanto una
sinusoide a 1000 Hz sintetizzata con il modulo oscil di
Csound (oscillatore a troncamento). L'unica differenza fra loro è la
lunghezza della tabella, che raddoppia sempre dal primo all'ultimo,
essendo 128, 256, 512, 1024, 2048, 4096, 8192.
Il sonogramma dovrebbe mostrare una singola linea, molto forte, a
1000 Hz, mentre, come si vede chiaramente, solo gli ultimi due
spettri (con tabella di 4096 e 8192 punti) sono abbastanza puliti.
Gli altri evidenziano delle componenti che non fanno parte del
segnale desiderato.
Si vede anche che le componenti indesiderate si attenuano via via
che la lunghezza della tabella aumenta. C'è da dire che, in realtà,
non spariscono mai del tutto, ma quando la loro ampiezza è 80 db
sotto al segnale primario, sono praticamente ininfluenti.
Quindi, un buon consiglio è: non usare tabelle inferiori a 4096
punti con un oscillatore audio a troncamento.
Oscillatore ad arrotondamento
Un sistema per ridurre l'errore dato dal troncamento è quello di
arrotondare la fase all'intero più prossimo, invece di troncarla del
tutto. Così, se la fase è 2.3, si prende il campione 2, mentre se è
2.8 si prende il 3. In termini di tempo di calcolo, basta sommare
0.5 alla fase istantanea, prima di troncarla. In tal modo, si resta
all'intero inferiore se la parte frazionaria della fase è < 0.5 e
si va a quello superiore se è >= 0.5.
La posizione di lettura in tabella è
int(fase_istantanea + 0.5)
Con questo sistema si possono utilizzare tabelle di lunghezza pari
alla metà del precedente, ma il risparmio di pochi kbyte non vale il
tempo perso per la somma e conviene passare a un sistema più
complesso, in grado di ridurre sensibilmente l'errore, come il
seguente.
Oscillatore a interpolazione
Con questo metodo si va a calcolare il valore presunto del campione
mediante una qualche forma di interpolazione fra i valori del
precedente e del successivo (eventualmente si possono considerare
più di due campioni).
Per esempio, se la fase è 5.3, si stima quale valore avrebbe un
ipotetico campione in 5.3, considerando il valore del campione 5 e
del 6, oppure, per una stima migliore, si possono prendere in
considerazione i valori dei campioni 4, 5, 6 e 7.
Chiaramente, con questi sistemi, il tempo di calcolo aumenta
notevolmente, però il risultato è molto più pulito anche con tabelle
relativamente corte.
I possibili sistemi di interpolazione sono molti. Qui tratteremo
solo quelli utilizzati in Csound e Max/MSP. Per una trattazione
generale, si veda la voce in
Wikipedia.
In pratica, interpolare significa trovare una funzione che passi per
i punti dati e poi calcolare il valore che questa funzione assume
nel punto richiesto. La funzione è un polinomio, cioè un'espressione
della forma:
y = K1xn + K2xn-1 + K3xn-2
+ ... + Knx + K
(per es. 2x4 - 5x3 + 6x2 + 7x - 3;
notare che i coefficienti Kn possono essere negativi)
Il metodo generale è quello di Lagrange che ha dimostrato che, dati
N punti, si può sempre trovare un polinomio di grado N-1 (cioè il
cui esponente massimo è N-1) che passa per tutti i punti dati. Di
conseguenza, se si considerano solo 2 punti, la funzione
interpolante è una retta (y = mx + p; grado 1) e abbiamo la
cosiddetta interpolazione lineare. Se si interpola su 4 punti, la
funzione è una cubica (y = K1x3 + K2x2
+ K3x + K; grado 3). Via via che il numero di punti su
cui si interpola aumenta, anche l'approssimazione migliora, ma
aumentano anche i calcoli necessari per definire la funzione e per
calcolare il valore richiesto.
Interpolazione lineare
 Questo
sistema approssima il valore del campione cercato, immaginando che i
punti della forma d'onda in tabella siano collegati da segmenti di
retta. In pratica, supponendo che si debba stimare il valore
dell'onda in 5.3 e che il campione 5 valga 10 e il campione 6 valga
20, nell'interpolazione lineare si immagina che, in questo
intervallo, l'onda cambi linearmente (appunto), passando da 10 a 20.
Di conseguenza, nel punto 5.1 varrà 11, in 5.2 varrà 12, in 5.3 13,
in 5.4 14, ... , in 5.9 19.
Questo
sistema approssima il valore del campione cercato, immaginando che i
punti della forma d'onda in tabella siano collegati da segmenti di
retta. In pratica, supponendo che si debba stimare il valore
dell'onda in 5.3 e che il campione 5 valga 10 e il campione 6 valga
20, nell'interpolazione lineare si immagina che, in questo
intervallo, l'onda cambi linearmente (appunto), passando da 10 a 20.
Di conseguenza, nel punto 5.1 varrà 11, in 5.2 varrà 12, in 5.3 13,
in 5.4 14, ... , in 5.9 19.
Quindi, per la posizione 5.3 l'oscillatore a interpolazione lineare
assumerà un valore di 13.
Il problema di questo metodo, però, è che l'interpolazione lineare è
una buona approssimazione solo se la funzione (in questo caso,
l'onda) non ha curve 5 molto pronunciate.
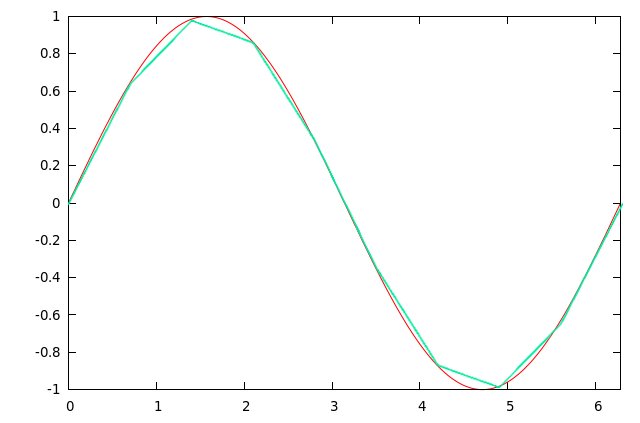
L'immagine a lato, che si ingrandisce cliccandola, mostra una
sinusoide (in rosso) e la sua approssimazione con un certo numero di
segmenti (in cyan).
Come si vede, in alcune parti la curva e la sua approssimazione
coincidono abbastanza bene, mentre in altre, dove la funzione è più
curva, divergono nettamente. Considerate che funzioni con armonici
hanno curve più pronunciate rispetto alla singola sinusoide.
L'errore dell'approssimazione dipende dalla funzione in tabella e
dal punto in cui ci si trova. In generale, comunque, l'errore medio
dipende dalla distanza che separa i due punti, quindi, anche qui, si
riduce con tabelle più lunghe. Il risultato è comunque nettamente
migliore rispetto all'oscillatore a troncamento
In Csound, il modulo oscili e altri da lui derivati (e.g.
oscil1i) utilizzano l'interpolazione lineare. Si noti che
questi moduli necessitano di una tabella dotata di "wrap-around
guard point", cioè di un punto in più, posto alla fine, in cui è
duplicato il valore del primo campione, per avere un punto finale
con cui interpolare quando la fase eccede di una frazione la
lunghezza - 1.
In Max/MSP, cycle~ usa l'interpolazione lineare su una
tabella lunga 512 campioni dotata di "wrap-around guard point" come
sopra. La lunghezza della tabella è fissa e non può essere cambiata
dall'utente (per tabelle di lunghezza qualsiasi si usa wave~).
Interpolazione cubica
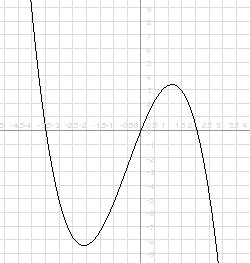 Il modulo oscil3 di
Csound utilizza, in via sperimentale, l'interpolazione cubica basata
su 4 punti (2 prima e 2 dopo). Nel caso di cui sopra (fase 5.3), la
funzione interpolante considera i valori dei campioni 4, 5, 6, 7.
Il modulo oscil3 di
Csound utilizza, in via sperimentale, l'interpolazione cubica basata
su 4 punti (2 prima e 2 dopo). Nel caso di cui sopra (fase 5.3), la
funzione interpolante considera i valori dei campioni 4, 5, 6, 7.
Con adeguati coefficienti, la cubica può assumere forme come quella
mostrata nella figura a destra, particolarmente adatte ad
approssimare sinusoidi o altre funzioni con curve pronunciate.
L'errore è decisamente inferiore rispetto a quello generato
dall'interpolazione lineare.
Considerazioni sull'interpolazione
Intanto, un confronto temporale. Nella seguente tabella trovate i
tempi di calcolo per la generazione di una sinusoide a 1000 Hz con
uno strumento composto da un solo oscillatore senza inviluppo con
out monofonico (vedi ex02.csd).
Per ogni modulo è stato generato un singolo suono di durata = 5000
secondi (circa 83 minuti) senza scrittura su disco (opzione -n).
L'operazione è stata ripetuta 5 volte, facendo, poi, la media dei
tempi (che comunque differivano di poco).
I tempi sono totali, cioè comprendono l'apertura e la chiusura del
job, compresa la compilazione dell'orchestra (solo 3 msec) e sono
stati calcolati con il comando unix time.
Il test è stato eseguito su un dual core a 2.2 Ghz con Ubuntu Linux
10.04 e Csound versione 5.10. Con altre macchine e/o sistemi si
potrebbero ottenere tempi diversi, ma, ribadisco, qui non c'entra la
velocità del disco rigido perché Csound è stato lanciato senza
scrittura (opzione -n). Quelli che vedete sono i tempi di puro
calcolo.
modulo
|
media |
percentuale |
| oscil |
4.35 |
100.00 |
| oscili |
5.46
|
125.52 |
| oscil3 |
8.42
|
193.56 |
Come si vede, rispetto all'oscillatore a troncamento, i tempi di
calcolo aumentano del 25% con l'interpolazione lineare e del 93% con
l'interpolazione cubica. Considerate che questo aumento è relativo
ad un solo oscillatore. Se in uno strumento ce ne sono più di uno,
l'aumento va moltiplicato.
Ora, però, è il caso di fare anche un test di qualità. Nella figura
seguente vedete lo spettro di una sinusoide a 1000 Hz generata con
tabella di 1024 punti da oscillatore a troncamento, interpolazione
lineare e cubica.
Si vede chiaramente come nel primo suono (troncamento) ci siano
componenti indesiderate, mentre gli altri due (interpolazione
lineare e cubica, rispettivamente) siano puliti.
Quindi, quale tipo di oscillatore conviene usare? A mio avviso, con
i computer attuali, conviene usare l'interpolazione lineare con
tabelle lunghe o il troncamento con tabelle lunghissime. Con una
tabella di 16777216 punti, la distanza fra un campione è il
successivo è di soli 0.000021458 gradi (0.000000375 radianti) che
corrisponde a uno scarto fra un valore e il successivo nell'ordine
di 10-7, quindi l'errore medio è piccolissimo.
Considerate che l'interpolazione è stata introdotta nei primi
software di sintesi per poter risparmiare memoria usando tabelle
corte. Quando, negli anni '70, lavoravo al CSC di Padova usando
l'antenato di Csound (il Music360 dello stesso Barry Vercoe), avevo
un'area di memoria di 256 Kb (kappa). Usarne 32 per una tabella di
8192 campioni (8192 * 4 byte) era uno spreco. Oggi il problema non
si pone e si possono tranquillamente utilizzare tabelle da 16 Mb
senza interpolazione risparmiando in tempo, che è una cosa non
recuperabile.
Altre particolarità
Frequenza negativa
Nell'oscillatore analogico una frequenza negativa non ha
significato. In quello digitale, invece, sì.
L'oscillatore si limita a calcolare il SI con la formula di cui
sopra e il fatto che F abbia un valore negativo significa soltanto
che anche SI è < 0. Nel caso già visto di F = 100 Hz, in cui il
SI era 2.32199546485, con F = -100 Hz sarà SI = -2.32199546485.
Grazie anche alla particolare codifica binaria degli interi negativi
e all'operazione di AND sulla lunghezza della tabella, questo
significa semplicemente che l'oscillatore scandirà la tabella
all'indietro, cioè non dal primo all'ultimo valore, ma dall'ultimo
al primo. Tutto ciò si traduce soltanto in un fatto: l'onda verrà
generata con fase invertita rispetto alla lettura normale. Di
conseguenza, l'esecuzione contemporanea di due suoni con la stessa
tabella e frequenza identica, ma una negativa, produce il nulla,
come si può vedere lanciando l'esempio ex04
6.
Questa particolarità è da ricordare perché, a volte, con certe
tecniche di sintesi, si generano delle componenti con frequenza
negativa, cioè con fase invertita.
Foldover
Come è noto, in digitale non si possono generare frequenze superiori
alla frequenza di Nyquist (ovvero SR/2). Per es., con SR = 44100,
non possono esistere frequenze > 22050. Ma cosa accade se si
chiede a un oscillatore di generare una frequenza > SR/2, per es.
30000 o 40000?
Esaminiamo in dettaglio il meccanismo di lettura.
Se la frequenza richiesta è < 22050 (SR/2), tutto procede
normalmente. Per es, con frequenza = 11000 e lunghezza tabella =
4096, abbiamo:
- frequenza di campionamento (SR) = 44100
- lunghezza tabella (TL) = 4096
- frequenza richiesta (F) = 11000 Hz
Con la formula già vista SI = TL * F / SR, abbiamo SI = 4096 * 11000
/ 44100 = 1021.67800454.
Questo valore corrisponde a circa ¼ della lunghezza della tabella.
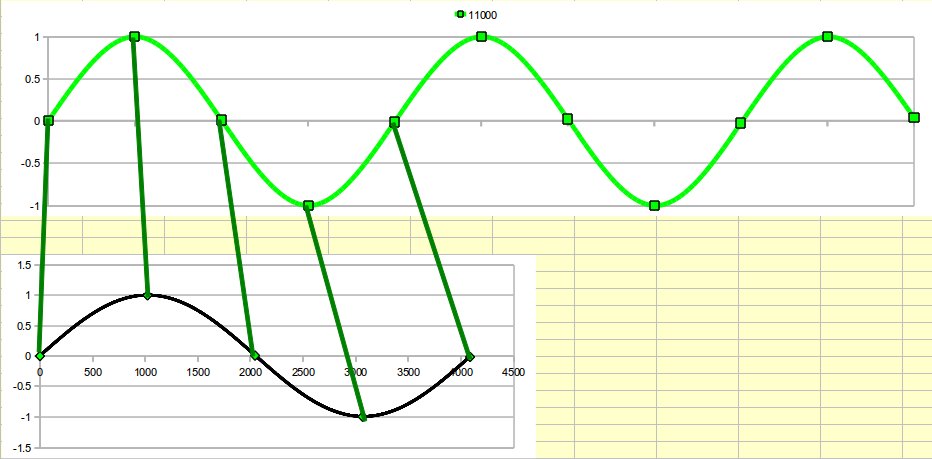
Di conseguenza la lettura procederà come in figura seguente. Sotto
(in nero) abbiamo la sinusoide memorizzata in tabella lunga 4096
campioni. Sopra (in verde), la sinusoide generata. Si vede come il
meccanismo proceda regolarmente: partendo dal primo campione procede
a passi di circa 1021 fino alla fine della tabella, per poi ciclare.
Ora, invece, chiediamo all'oscillatore di generare una frequenza
> SR/2.
L'oscillatore non si rifiuta. Come al solito calcola il suo SI e
procede, ma il SI sarà così grande che l'oscillatore produrrà solo
un campione per ciclo, o ancora meno, con l'effetto di non
riprodurre la forma d'onda in tabella, ma di generarne una a
frequenza inferiore perché troppe parti della tabella saranno
saltate.
Per esempio, sia
- frequenza di campionamento (SR) = 44100
- lunghezza tabella (TL) = 4096
- frequenza richiesta (F) = 40000 Hz
Con la formula già vista SI = TL * F / SR, abbiamo SI = 4096 * 40000
/ 44100 = 3715.19274376.
Con questo SI, il primo campione sarà a 0, il secondo a
3715.19274376 e il terzo a 7430.38548752. Ma quest'ultimo valore è
già ampiamente oltre la lunghezza della tabella, per cui si esegue
un ritorno a capo e si va al campione 7430.38548752 - 4096 =
3334.38548752.
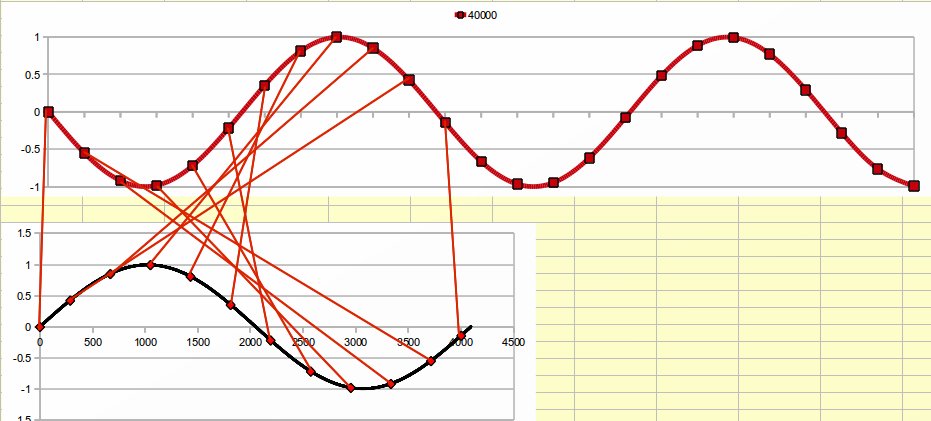
Quello che accade è schematizzato in figura sotto.
Come si vede, la situazione è un po' più strana rispetto alla
precedente. Come è normale, si parte dal primo campione, ma il
secondo (circa 3715) è così avanti da trovarsi vicino alla fine
della tabella. Di conseguenza, già con il terzo, che sarebbe a
7430.38548752, si ritorna a capo, andando al campione 7430.38548752
- 4096 =3334.38548752 e così via.
Una prima conseguenza, apprezzabile anche in figura, è che la fase
dell'onda è invertita, come se la tabella venisse letta
all'indietro. E in effetti è così: il SI è così grande che il punto
di lettura si muove, praticamente, all'indietro (un effetto analogo
si può vedere nei vecchi film western in bianco e nero, in cui la
frequenza dei fotogrammi era così bassa che le ruote delle diligenze
sembravano ruotare all'indietro).
Ma quello della fase è il problema minore. Il problema maggiore è
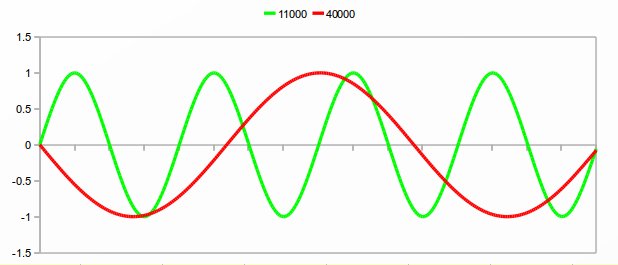
che, in tal modo, il ciclo non viene riprodotto correttamente. Se,
infatti, sovrapponiamo le due onde così generate, mettendole nella
giusta scala, vediamo (fig. sotto) che l'onda a 40000 Hz (rossa) ha
un periodo ben più lungo di quella a 11000 (verde). Se ne deduce che
l'onda generata ha frequenza inferiore a quella prevista.
Questo accade perché il SI dell'onda a 40000 Hz è così grande che
non è in grado di campionare adeguatamente l'onda in tabella
prendendo un solo campione per ogni ciclo, mentre ne sarebbero
necessari almeno due.
Per spiegare la cosa con una analogia, è come se, dovendo fare un
grafico della variazione di temperatura nella vostra città, voi
andaste a misurarla solo una volta al giorno, mentre invece, per
avere un risultato realistico, avete bisogno almeno di due misure:
una nella zona di massimo (per es. alle 14) e una in quella di
minimo (es. dopo mezzanotte). Se invece leggete le temperature solo
di giorno (o di notte) otterrete un grafico che sovrastima
(sottostima) il valore medio.
In modo analogo, anche nel caso dell'oscillatore digitale servono
almeno due campioni per ciclo per poter riprodurre una forma d'onda
con la frequenza corretta, altrimenti avremo un errore. Notare che
il limite dei due campioni per ciclo si raggiunge proprio con
frequenza pari a SR/2, infatti, dalla formula già vista, SI = TL * F
/ SR, abbiamo SI = TL * SR/2 / SR = TL * SR / 2 * SR = TL / 2.
Alla frequenza di SR/2, quindi, il SI è pari a metà della lunghezza
della tabella. Oltre questa frequenza SI > TL/2, quindi abbiamo
meno di un campione per ciclo. Di conseguenza, oltre questo muro, la
frequenza prodotta differisce quella richiesta.
È facile calcolare qual'è la frequenza effettivamente prodotta:
basta sottrarla da SR. Infatti, se freq > SR/2, la frequenza
effettiva è SR - freq.
Es. sia SR 44100 e si chiede freq = 30000, il risultato è una
frequenza = 44100 - 30000 = 14100.
Questo fenomeno è detto foldover (ripiegamento della parte che sta
sopra), infatti la parte di frequenza che eccede SR/2 si ripiega
intorno a SR/2. In pratica, rimbalza indietro, come se il valore
SR/2 fosse un muro (come effettivamente è).
A titolo di esempio, ascoltate questo suono creato con Csound, che
contiene un semplice oscillatore sinusoidale la cui frequenza glissa
con continuità superando il valore di SR/2. Per non mettere a dura
prova il vostro udito, qui la frequenza di campionamento è 22050 e
la frequenza della sinusoide va da 5000 Hz a 20000 Hz in 20 secondi.
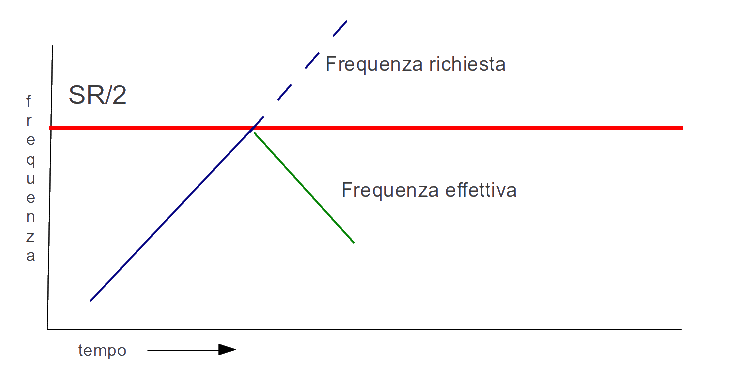
Si dovrebbe sentire un glissato sempre ascendente, mentre, a un
certo punto (a SR/2 = 11025 Hz), la frequenza comincia a scendere,
come schematizzato in figura. Sono in ogni caso frequenze alte:
attenzione alle orecchie. Clicca qui per
ascoltare l'esempio e qui per vedere
il codice Csound.
Ovviamente bisogna fare i conti con il foldover considerando non
solo la fondamentale, ma anche tutte le componenti del nostro suono.
Se, per esempio, stiamo lavorando con una forma d'onda che contiene
una ventina di armonici, bisogna pensare che a 1000 Hz il ventesimo
armonico è già a 20000 Hz e di conseguenza, con SR = 44100, si
produrrà foldover già quando la fondamentale raggiunge i 1102.5 Hz.
[1] Si può pensare che Csound si comporti
così perché, di solito, non viene utilizzato in tempo reale, ma
scrive in un file. Ebbene, non è così. Anche i software concepiti
per il real time, sebbene siano "interrupt driven" (come Max/MSP),
contano solo i campioni e seguono solo in parte il tempo reale. Il
loro legame con quest'ultimo è, sì, determinato dall'interrupt, ma
i software lavorano in un "tempo logico" che
è leggermente sfasato rispetto al tempo reale. Questo perché
devono riempire di campioni audio un piccolo buffer prima
che i suddetti campioni debbano essere spediti al DAC (in Max/MSP
la dimensione di tale buffer è l'I/O Vector Size controllabile dal
box DSP Status).
Di conseguenza sono in ritardo rispetto
al tempo reale (è la cosiddetta latenza). Ciò accade perché, in
questo preciso istante, il software sta, in realtà, calcolando i
prossimi (per es.) 10 millisecondi di suono. Ne consegue che, se
un evento audio esterno (es. l'input da un microfono) arriva
adesso, il suo effetto si sentirà solo fra 10 millisecondi, cioè
quando il buffer che adesso è in via di riempimento verrà mandato
in output (ricordo chiaramente il piccolo shock che questa cosa mi
ha provocato quando, ai tempi dell'Apple II, ho scritto in
assembler il mio primo scheduler di eventi audio per le schede
della Mountain Hardware).
Ma tutto questo, ormai, è accademia. Chi volesse approfondire può
consultare, fra gli altri, il testo di Miller Puckette "The Theory
and Technique of Electronic Music", cap. 3.2, pag. 61 segg.
[2] Incidentalmente,
questa è anche la ragione per cui non si possono mixare via
software segnali a SR diverso e se un software lo fa, esegue una
conversione preventiva senza dirvelo. Sempre incidentalmente,
questo è quello che accade ogni volta che un sistema operativo
riproduce suoni con la scheda audio in dotazione: tutti i segnali
vengono convertiti al SR di quella scheda (tipicamente 48000 per
le schede on-board).
[3] In Max/MSP, per
certi moduli, il minimo intervallo temporale dipende anche da
altri fattori, come la dimensione del vettore di I/O.
[4] Ovviamente è più
elegante dire dove il coefficiente angolare della derivata prima è
maggiore.
[5] Modo di dire per
spiegare la cosa a chi è digiuno di matematica. Ovviamente si
dovrebbe guardare la derivata seconda.
[6] Qualcuno si
chiederà perché l'ampiezza totale viene ad essere 23 e non 0. Il
fatto è che le due onde sono, sì, in fase invertita l'una rispetto
all'altra, ma hanno anche un campione di differenza. Questo perché
il primo campione della tabella ha fase 0, ma l'ultimo campione
non ha fase 360° (2π), bensì 360 meno un campione.






 Guardando
la
figura
a
lato,
relativa
a
una
semplice
sinusoide
campionata
in
128
passi,
si
vede a occhio nudo come la differenza fra un campione e il
successivo non sia sempre uguale, ma aumenti dove la funzione ha
pendenza maggiore (ovvero, dove i gradini sono più alti) 4.
Guardando
la
figura
a
lato,
relativa
a
una
semplice
sinusoide
campionata
in
128
passi,
si
vede a occhio nudo come la differenza fra un campione e il
successivo non sia sempre uguale, ma aumenti dove la funzione ha
pendenza maggiore (ovvero, dove i gradini sono più alti) 4.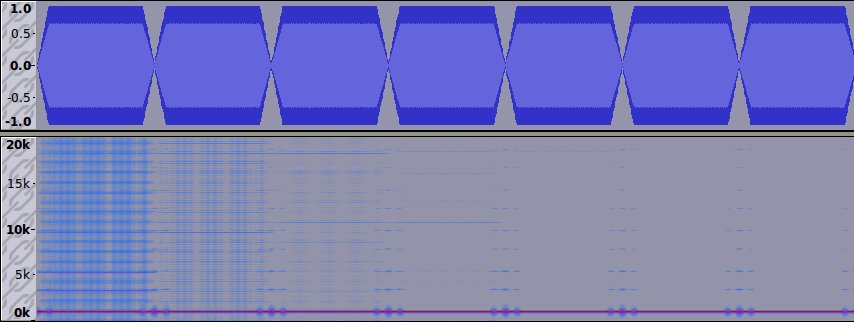
 Questo
sistema approssima il valore del campione cercato, immaginando che i
punti della forma d'onda in tabella siano collegati da segmenti di
retta. In pratica, supponendo che si debba stimare il valore
dell'onda in 5.3 e che il campione 5 valga 10 e il campione 6 valga
20, nell'interpolazione lineare si immagina che, in questo
intervallo, l'onda cambi linearmente (appunto), passando da 10 a 20.
Di conseguenza, nel punto 5.1 varrà 11, in 5.2 varrà 12, in 5.3 13,
in 5.4 14, ... , in 5.9 19.
Questo
sistema approssima il valore del campione cercato, immaginando che i
punti della forma d'onda in tabella siano collegati da segmenti di
retta. In pratica, supponendo che si debba stimare il valore
dell'onda in 5.3 e che il campione 5 valga 10 e il campione 6 valga
20, nell'interpolazione lineare si immagina che, in questo
intervallo, l'onda cambi linearmente (appunto), passando da 10 a 20.
Di conseguenza, nel punto 5.1 varrà 11, in 5.2 varrà 12, in 5.3 13,
in 5.4 14, ... , in 5.9 19. Il modulo oscil3 di
Csound utilizza, in via sperimentale, l'interpolazione cubica basata
su 4 punti (2 prima e 2 dopo). Nel caso di cui sopra (fase 5.3), la
funzione interpolante considera i valori dei campioni 4, 5, 6, 7.
Il modulo oscil3 di
Csound utilizza, in via sperimentale, l'interpolazione cubica basata
su 4 punti (2 prima e 2 dopo). Nel caso di cui sopra (fase 5.3), la
funzione interpolante considera i valori dei campioni 4, 5, 6, 7.