Mauro Graziani - Dispense di Acustica per Musicisti

Acustica 04
Misurare l'onda: la frequenza
Cicli e altezze
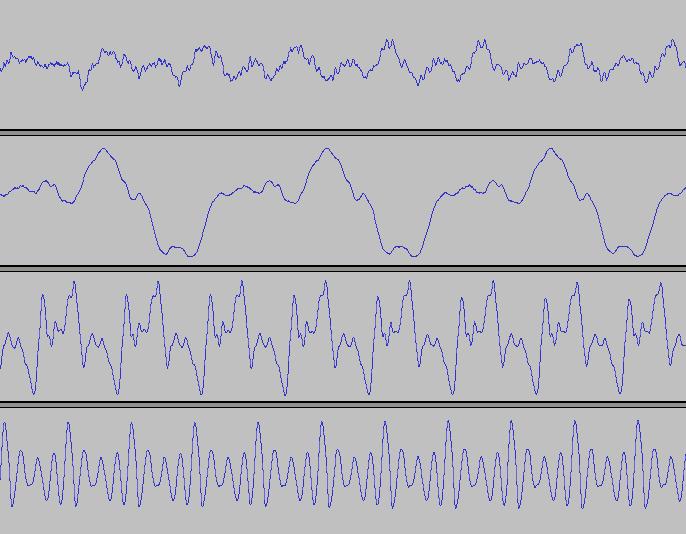
Arriviamo finalmente alle onde. Nella figura seguente potete vedere un
frammento delle onde prodotte da una nota singola di
pianoforte, violoncello,
clarinetto, oboe
(dall'alto al basso, potete ascoltare questi suoni cliccando sui nomi).
Si nota subito che l'andamento di queste onde non è casuale. Esiste un
ciclo che si ripete di continuo, con lievi differenze. Queste onde sono
periodiche.
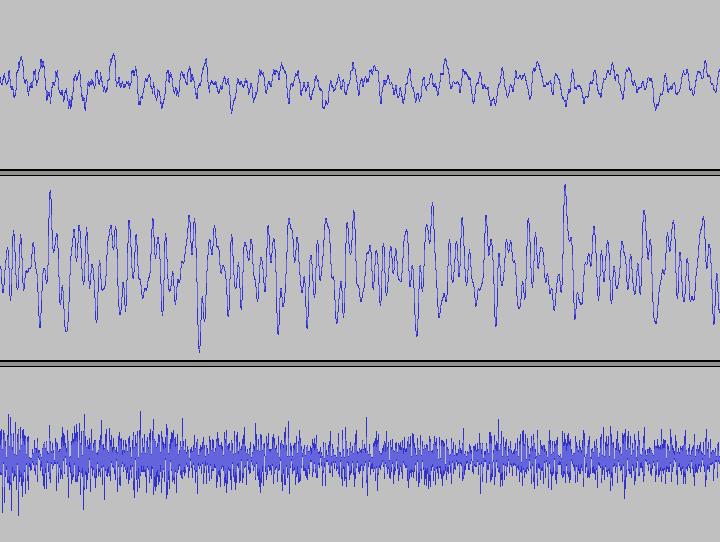
Ora osservate queste onde tratte da un
gong, un
suono
elettronico tipo campana, un
piatto
di batteria.
Noterete che, a differenza delle prime, in queste onde non è possibile
individuare con facilità un ciclo. C'è una notevole differenza con
quelle dell'immagine precedente in cui la periodicità è molto evidente.
Ascoltando questi suoni, vi accorgerete subito che, a differenza dei
precedenti, non è possibile attribuire loro una nota precisa. I primi
due vengono percepiti quasi come un accordo, mentre l'ultimo suggerisce
solo vagamente una sensazione di altezza.
Qualcuno, a questo punto, si chiederà se
esiste un collegamento fra la periodicità dell'onda e la
sensazione di altezza?
Per il momento possiamo solo rispondere: in linea di massima,
sì. Ci occuperemo in dettaglio di questo problema quando parleremo di
armonici, comunque ne accenniamo perché, secondo i vecchi manuali di
acustica, la periodicità dell'onda era una condizione indispensabile
perché quel suono avesse una altezza precisa, tanto che questi suoni
erano chiamati "suoni musicali", opposti ai cosiddetti "rumori" (suoni
non musicali, non periodici, privi di altezza).
Oggi sappiamo che questa distinzione non ha valore perché non è così
netta, ma è un continuum: si può passare gradualmente dalla sensazione
di altezza precisa a una sensazione di altezza sempre più vaga fino a
perderla. Pensate, per es., al soffio in uno strumento a fiato
(flauto, clarinetto, sassofono): se si soffia senza produrre una nota e
si aprono, via via, le chiavi, il soffio cambia, suggerendo una
altezza. Oppure pensate alle campane che spesso sono "quasi note", cioè
danno una sensazione di altezza, ma con dentro qualcosa di leggermente
stonato. Ancora, ascoltate e guardate nella figura seguente
questi due suoni che contengono una
certa quantità di rumore. Noterete che la sensazione di altezza è meno
precisa nel secondo rispetto al primo, ma c'è. Noterete anche,
guardando la figura, che una periodicità esiste, ma non è così precisa.
In definitiva, pur con qualche eccezione, possiamo dire che
- un onda strettamente periodica produce quasi certamente una
sensazione di altezza
- via via che la periodicità dell'onda diventa meno stretta,
anche la sensazione di altezza è meno precisa
Misurare l'onda
Ora vedremo che cosa è possibile misurare con precisione in un'onda.
Consideriamo una forma d'onda strettamente periodica.
Per prima cosa è possibile misurare la lunghezza di un ciclo, la sua
durata e il numero di volte che esso si ripete in un secondo. La
lunghezza è un valore raramente utilizzato in acustica musicale (serve
invece nel campo delle trasmissioni radio). Concentriamoci, quindi
sulle ultime due misure.
- Durata del ciclo o Periodo:
il periodo è la durata di un ciclo e si misura in frazioni di secondo
- Frequenza:
il numero di ripetizioni del ciclo per secondo. Si misura in Hertz
(abbr. Hz). Un'onda il cui ciclo si ripete 100 volte al secondo ha una
frequenza di 100 Hertz è strettamente collegata all'altezza
del suono.
Nota: in inglese,
come misura della frequenza si usa anche la
definizione CPS (Cycles Per Second). Ovviamente 1 CPS = 1 Hertz.
Chiaramente, il Periodo e la Frequenza sono strettamente
collegati: se il ciclo di un'onda si ripete 100 volte al secondo, ogni
ciclo dura necessariamente 1/100 di secondo. Quindi il Periodo è uguale
a 1/Frequenza e la Frequenza = 1/Periodo.
- Ampiezza: è
lo scostamento dell'onda dalla linea di zero (non suono). Si misura in
deciBel. Come vedremo più avanti, è legata alla
dinamica/intensità/volume del suono.
- Fase: la fase, in un certo punto, è
l'istante in cui l'onda si trova nel ciclo. Il ciclo ha una certa
forma; in ogni istante, l'onda si trova in un punto di quel ciclo:
questa è la fase. Si misura in gradi (da 0 a 360, come un angolo)
o in radianti (da 0 a 2 pi-greco; c'è un legame fra le onde e la
trigonometria, ma sorvoliamo). Per vostra fortuna, nel caso di suoni
singoli, l'orecchio è insensibile alla fase, quindi, per il momento non
ci serve, ma la troveremo nei battimenti.
La figura visualizza queste misure. La frequenza e l'ampiezza sono le
misure che utilizzeremo più spesso.

Frequenza e Altezza
Come già accennato, frequenza e altezza sono strettamente collegate. In
effetti, tutti noi ci accordiamo sul LA 440 Hz. In breve, per ogni nota
c'è una frequenza.
Innanzi tutto, la frequenza permette di definire con precisione il
nostro campo udibile.
Gli umani
sentono frequenze da circa 16 a circa 20.000 Hz
La soglia superiore si abbassa rapidamente con l'età e l'usura (chi
ascolta spesso suoni molto forti perde frequenze alte più rapidamente
del normale).
Ma quanta di questa estensione noi utilizziamo effettivamente in
musica? In termini di note, solo una parte (circa 1/4), ma in realtà
quasi tutta, perché sopra a ogni suono ci sono gli armonici.
A titolo di esempio, in questa tabella, trovate le frequenze
corrispondenti alle note del sistema temperato (evidenziata
l'estensione del pianoforte).
|
-1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
C
|
16.35
|
32.70
|
65.41
|
130.81
|
261.63
|
523.25
|
1046.50
|
2093.00
|
4186.01
|
8372.02
|
|
C#/Db
|
17.32
|
34.65
|
69.30
|
138.59
|
277.18
|
554.37
|
1108.73
|
2217.46
|
4434.92
|
8869.84
|
|
D
|
18.35
|
36.71
|
73.42
|
146.83
|
293.66
|
587.33
|
1174.66
|
2349.32
|
4698.64
|
9397.27
|
|
D#/Eb
|
19.45
|
38.89
|
77.78
|
155.56
|
311.13
|
622.25
|
1244.51
|
2489.02
|
4978.03
|
9956.06
|
|
E
|
20.60
|
41.20
|
82.41
|
164.81
|
329.63
|
659.26
|
1318.51
|
2637.02
|
5274.04
|
10548.08
|
|
F
|
21.83
|
43.65
|
87.31
|
174.61
|
349.23
|
698.46
|
1396.91
|
2793.83
|
5587.65
|
11175.30
|
|
F#/Gb
|
23.12
|
46.25
|
92.50
|
185.00
|
369.99
|
739.99
|
1479.98
|
2959.96
|
5919.91
|
11839.82
|
|
G
|
24.50
|
49.00
|
98.00
|
196.00
|
392.00
|
783.99
|
1567.98
|
3135.96
|
6271.93
|
12543.85
|
|
G#/Ab
|
25.96
|
51.91
|
103.83
|
207.65
|
415.30
|
830.61
|
1661.22
|
3322.44
|
6644.88
|
13289.75
|
|
A
|
27.50
|
55.00
|
110.00
|
220.00
|
440.00
|
880.00
|
1760.00
|
3520.00
|
7040.00
|
14080.00
|
|
A#/Bb
|
29.14
|
58.27
|
116.54
|
233.08
|
466.16
|
932.33
|
1864.66
|
3729.31
|
7458.62
|
14917.24
|
|
B
|
30.87
|
61.74
|
123.47
|
246.94
|
493.88
|
987.77
|
1975.53
|
3951.07
|
7902.13
|
15804.27
|
Da questa tabella possiamo dedurre delle cose interessanti. Se, per
esempio, osservate la riga del LA (A) noterete che lo scarto di
frequenza tra le varie ottave non è costante (più piccolo nelle ottave
basse, più grande in quelle alte). Tuttavia noi sentiamo una differenza
costante, sempre una ottava. E allora?
Notate che, se non è costante la differenza, è invece costante il
rapporto:
la frequenza dell'ottava superiore è sempre il doppio di quella
inferiore.
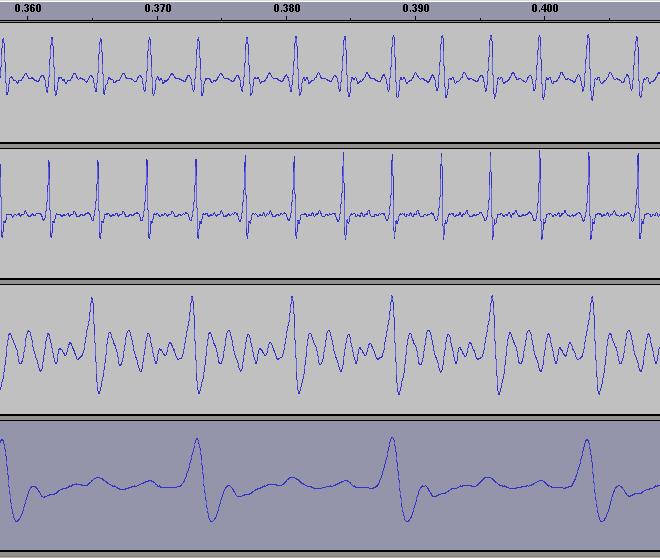
La cosa è ben visibile in questa immagine che rappresenta onde della
famiglia degli ottoni: dall'alto al basso, corno, tromba, trombone,
tuba.
Si vede bene che corno e tromba stanno eseguendo la stessa nota,
infatti la durata del ciclo è identica (i picchi corrispondono). Il
trombone è una ottava sotto la tromba, infatti ogni suo ciclo
corrisponde a due della tromba. Il tuba è una ottava sotto il trombone
e due sotto la tromba, infatti ogni suo ciclo corrisponde a due del
trombone e a 4 della tromba.
L'ottava, quindi, corrisponde a un
rapporto di frequenza 2:1. La cosa ha una precisa corrispondenza
fisica: dividendo una corda a metà, si ottiene l'8va superiore (corde
più corte producono frequenze più alte in base al loro rapporto; la
barretta del 12mo tasto della chitarra si trova a metà corda).
Nello stesso modo funzionano le colonne d'aria: se si prende un tubo e
lo si suona in stile flauto di pan, si ottiene una nota. Se si taglia a
metà il tubo, si ottiene l'8va superiore.
Anche per gli altri intervalli ci sono rapporti fissi. Nella scala
pitagorica, direttamente derivata dagli armonici, alla 5a corrisponde
il rapporto di 3:2 = 1.5. Ne consegue che, dato un LA 440 Hz, il MI
alla 5a sopra avrà una frequenza di 440 x 1.5 = 660.
Ma, un momento; se guardiamo il MI sopra il La 440 nel sistema
temperato, vediamo che non è 660, ma 659.26. Il fatto è che, come
saprete, la scala costruita sugli armonici conduce direttamente ai
semitoni non coincidenti, al DO# diverso dal REb, cosa che il
temperamento equabile ha eliminato, con il prezzo di approssimare gli
intervalli. La tabella seguente mostra l'approssimazione per alcuni
intervalli maggiori
Intervallo
|
Temp.
equabile
|
Scala
Pitagorica
|
Rapporto
Pitagorico
|
2a
|
1.1224
|
1.125
|
9/8
|
3a
|
1.26
|
1.25
|
5/4
|
4a
|
1.3348
|
1.333...
|
4/3
|
5a
|
1.4983
|
1.5
|
3/2
|
6a
|
1.6818
|
1.666...
|
5/3
|
Allora, qual'è il rapporto che equivale a un semitono nel sistema
temperato? Bene, si tratta di dividere il rapporto 2:1 (l'ottava) in 12
parti
uguali, ognuna corrispondente a un semitono. Il risultato è
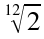 =
1.0594631 (approssimato)
=
1.0594631 (approssimato)
Al di là dei numeri (che non dovete
sapere a memoria), qual è l'importanza di tutto ciò?
per
la percezione sono importanti i rapporti di frequenza
Ovvero, noi
percepiamo sempre lo stesso intervallo quando il
rapporto fra le frequenze è costante. Partendo da un LA 110
Hz, per percepire un intervallo di 8va dobbiamo raddoppiarlo andando a
220 Hz, poi a 440 Hz, a 880 Hz e così via. Per ottenere la 5a superiore
dobbiamo moltiplicarlo per 1.5 = 165 Hz, eccetera.
Ciò che
resta costante è il
rapporto, non la differenza.
A questo punto punto abbiamo anche bisogno di una unità di misura degli
intervalli, cioè una unità basata sui rapporti. Ovviamente è il più
piccolo intervallo che usiamo, cioè il semitono, infatti le scale e gli
intervalli sono definiti in termini di semitoni.
Volendo misurare una differenza minore di un semitono possiamo
utilizzare il
cent che equivale a
1/100 di semitono (1 semitono = 100 cent, 1/4 di tono = 50 cent).
La Percezione della Frequenza
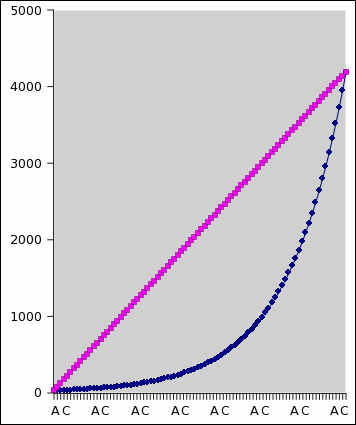 Una scala cromatica, per noi, equivale a una
scala con gradini tutti uguali, praticamente una linea retta, come la
linea in rosso nella figura a destra.
Una scala cromatica, per noi, equivale a una
scala con gradini tutti uguali, praticamente una linea retta, come la
linea in rosso nella figura a destra.
Se però, guardiamo questa scala in termini di frequenze, segnando sul
grafico la frequenza in Hz che corrisponde a ogni semitono, otterremo
la linea blu che invece è una particolare curva detta esponenziale.
La differenza fra le due linee è netta ed è anche strutturale: si
ha
una retta quando ogni punto è il precedente più qualcosa (somma) mentre
si ottiene un esponenziale quando ogni punto è il precedente per
qualcosa (moltiplicazione).
In pratica, noi sentiamo una retta quando in realtà abbiamo una curva.
Questo comportamento non è limitato solo all'acustica, ma si trova
spesso quando abbiamo a che fare con il sistema percettivo.
In questo caso, è dovuto al modo in cui le frequenze vengono mappate
dall'organo del Corti all'interno della chiocciola. È stato osservato,
infatti, che le onde generate dalle basse frequenze si spingono più
avanti nella chiocciola, mentre le alte frequenze si esauriscono prima.
In tal modo, le cellule poste all'inizio della chiocciola sono
interessate solo dalle alte frequenze. Le onde generate dalle frequenze
più basse, invece, riescono a penetrare di più e vanno a toccare anche
cellule che stanno più all'interno della chiocciola.
In pratica, l'organo del Corti è un raffinato analizzatore che scompone
il suono nelle sue componenti basse, medie e alte inviando al cervello
informazioni differenziate per ogni registro.
Se si va a vedere quali cellule rispondono alle diverse ottave, si nota
che la loro distanza è all'incirca uguale.
La figura sotto mostra la distanza percorsa all'interno della
chiocciola dalle onde generate da diverse frequenze. Le onde di
frequenza pari al LA7 (3520 Hz) penetrano per circa 12 mm, quelle del
LA6 per circa 17 mm, quelle del LA5 per circa 22 mm e così via. Si nota
che un salto di 8va corrisponde a circa 4 mm all'interno della
chiocciola. Di conseguenza un salto di frequenza variabile in termini
di Hertz, come quello dell'8va, quando arriva all'organo del Corti
viene mappato su uno spazio all'incirca sempre uguale, come nella
figura sotto. Si ritiene che questa sia la ragione per cui noi
percepiamo come identici gli intervalli, cioè i rapporti e non le
differenze di frequenza.
Notate anche un'altra cosa. L'estensione
di frequenze che va approssimativamente da 20 Hz fino a 4000 Hz copre
circa i due terzi dell'estensione della membrana basilare (dai 12 ai 35
mm dalla base) su cui risiede l'organo del Corti. La rimanente porzione
della scala di frequenze (4000 - 16000 Hz) è compressa nel rimanente
terzo. Ne consegue che, in quest'ultima parte, composta da suoni che
noi giudichiamo acutissimi, la percezione è più difficoltosa, meno
sicura, in ogni caso meno precisa.
Ora, notate come il range di frequenze fra 20 e 4000 Hz corrisponde
alle prime 7 ottave musicali, riconosciute come le più importanti in
musica. Non a caso corrisponde esattamente all'estensione del
pianoforte. Quindi, la nostra musica si è conformata alle capacità del
nostro sistema percettivo (ovviamente).
Soglia della discriminazione di frequenza
Qual'è la minima differenza di frequenza
che riusciamo a percepire? Anche qui la risposta è un po' più complessa
di quanto si potrebbe pensare.
Innanzitutto dobbiamo distinguere due casi molto diversi: frequenze
successive (l'una inizia dopo la fine dell'altra) e simultanee (suonano
insieme).
Nota: nei testi inglesi la soglia di discriminazione della frequenza è
chiamata JND (Just Noticeable Difference: minima differenza percepibile)
Frequenze successive
In questo caso la differenza minima non è fissa. Dipende da due cose:
- l'altezza: è più semplice accorgersi di una
differenza in frequenza sopra i 1000 Hz che a frequenze più basse
(questo perché, come vedremo, è la zona in cui l'orecchio funziona
meglio)
- la dinamica: se il suono è ppp è più difficile notare la
differenza rispetto a mf o
superiore.
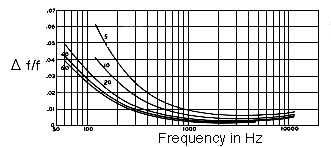
In figura vediamo le curve di discriminazione della frequenza per
diverse ampiezze in db scritte vicino alla curva. La minima differenza
percepibile è espressa come rapporto fra le due frequenze. Il fatto che
le curve si alzino in corrispondenza delle frequenze sotto ai 1000 Hz
significa che, per discriminare in questa zona, occorrono differenze
maggiori.
Per esempio, a 1000 Hz, con dinamica 60 db (circa
mf), viene percepita una differenza
pari a circa lo 0.002, il che significa 2 Hz (1000 * 0.002 = 2).
Quindi, avendo due suoni successivi, il primo di 1000 Hz e l'altro
almeno a 1002 o 998, si dovrebbe percepire la differenza. Con dinamica
più bassa, per es. a 10 db (appena percettibile), la soglia sale a
circa lo 0.006, cioè 6 Hz.
A frequenze più basse, le cose cambiano. A 100 Hz e 60 db serve circa
lo 0.26 cioè 2.6 Hz di differenza. A 100 Hz e 10 db la differenza non è
avvertibile.
In
questo esempio audio potete
sentire varie coppie di frequenze in cui la prima è sempre 1000 Hz
mentre la seconda aumenta sempre di 1 Hz (1001, 1002, 1003, etc).
Potete sperimentare quando riuscite a notare la differenza.
Avete fatto l'esperimento? Se siete
riusciti a notare una differenza già alla prima coppia di frequenze
siete dei mentitori perché sono uguali. Nella seconda, la differenza è
1 Hz, nella terza è 2 Hz e così via.
Frequenze simultanee
Nel caso di frequenze simultanee, la discriminazione richiede una
differenza maggiore. La percezione simultanea di più frequenza investe
vari argomenti come quello della banda
critica, dei battimenti e dei suoni di combinazione, come il terzo
suono.
Il problema è quello del potere di risoluzione dell'orecchio, cioè
della capacità di distinguere due frequenze simultanee. Questa faccenda
è complicata anche dalle varie interferenze che si formano nel liquido
della chiocciola quando cominciano a circolare contemporaneamente onde
diverse.
Per chiarire, vediamo prima un esempio relativo all'occhio. Nella
figura qui
sotto, varie linee bianche e nere diventano sempre più sottili. Quando
le linee sono abbastanza grosse, si distinguono bene. Quando diventano
più sottili si entra in una zona di incertezza. Alla fine, non si
distinguono più e si
vede una barra grigia, cioè la media fra bianco e nero.
Questo accade perché, ad un certo punto, le linee diventano così
piccole che vanno a stimolare lo stesso gruppo di cellule sulla retina.
Per questa ragione, l'occhio non riesce più a differenziarle. Accade la
stessa cosa anche con il tatto: se non si guarda, due punture
di spillo molto vicine sembrano nello stesso punto.
Come vedremo ora, nell'orecchio accade una cosa simile.
 Banda critica
Banda critica
Introduciamo ora il concetto di Banda
Critica che è molto importante perché determina sia la percezione di
suoni simultanei (accordi) che quella del timbro.
Esso, inoltre, ha influenzato vari aspetti della pratica musicale, come
vedremo.
Abbiamo visto che l'orecchio interno è
un potente analizzatore in grado di distinguere le componenti di un
suono. La sua capacità di discriminazione ha però dei limiti.
Le cellule dell'organo del Corti che interpretano le informazioni di
frequenza, infatti, lavorano a gruppi di circa 1300, ognuno dei quali
occupa fisicamente circa 1.3 mm di membrana basilare e copre, in
frequenza, circa 1/3 di ottava.
Ognuno di tali gruppi costituisce una Banda Critica
(Critical Band).
Quando due frequenze simultanee sono abbastanza vicine da stimolare lo
stesso gruppo di cellule e quindi cadono entrambe entro la stessa banda
critica, la loro distinzione diventa difficile, se non impossibile e dà
luogo a vari fenomeni.
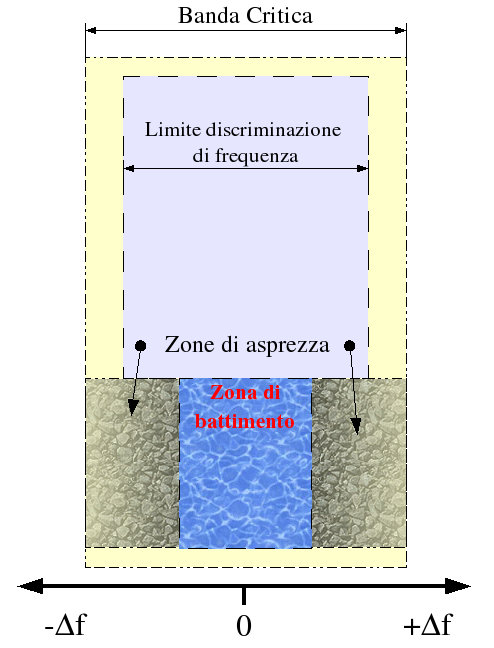
Questo esempio sonoro e la
figura a fianco spiegano che cosa accade in pratica. Partiamo con due
frequenze uguali e mentre una rimane fissa, l'altra si alza in
glissando.
All'inizio non avrete la sensazione di due frequenze, ma di un solo
suono. Via via che la seconda frequenza si allontana dalla prima,
sentirete:
- battimenti, che diventano più rapidi fino a
- un suono aspro (rough), sempre senza distinguere le due frequenze
(avrete sempre la sensazione di un unico suono).
- Solo quando la loro differenza supererà una certa soglia di
discriminazione (il limite di discriminazione di due frequenze
simultanee, circa 15 Hz), inizierete a distinguere le due frequenze,
pur
permanendo la sensazione di suono aspro.
- Quando, infine, verrà superata una seconda soglia pari al limite
della banda critica, finirà la sensazione di asprezza.
Se ne deduce che
quando due suoni
simultanei sono interni alla banda critica danno luogo a uno dei
seguenti fenomeni:
battimenti
suono aspro
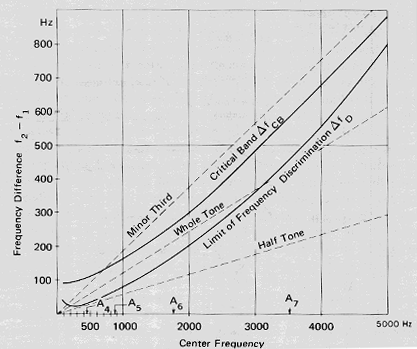
A questo punto è molto importante capire quanto è larga la banda
critica. La figura sotto ci mostra che, nella maggior parte dello
spettro sonoro, la sua estensione è un po' più di un tono e un po' meno
di una 3a minore sia in più che in meno rispetto a una qualsiasi
frequenza centrale. Ciò significa che, se prendiamo un LA come
frequenza centrale, la banda critica andrà all'incirca dal SOL fino al
SI.
L'intervallo
coperto da una banda critica è circa 1/3 di ottava.
Intanto notate che il tono e quindi anche il semitono sono sempre
dentro la banda critica. Questo spiega perché i bicordi di 2a mag. e
min. danno sempre una sensazione aspra. Spiega anche perché nei
"cluster" di semitoni e toni (cluster = accordo formato da varie note a
distanza di semitono o tono) non si distinguono i singoli suoni, mentre
invece si distinguono benissimo in un accordo di terze sovrapposte.
Notate inoltre che nella parte bassa
dello spettro sonoro, la banda critica è un po' più larga, tanto da
includere anche la 3a minore (e nella parte bassissima, anche la 3a
mag). Questa spiega perché, sui bassi, un bicordo di 3a suona male e
anche perché, nella pratica del contrappunto, si lascia sempre un certo
spazio fra il basso e le altre voci.
Battimenti
Ora vediamo un po' più in dettaglio alcuni
fenomeni legati alla banda critica.
I battimenti possono essere di due tipi
Battimenti di prima specie (o primo ordine)
Un battimento di prima specie è provocato da due suoni con frequenze
molto vicine, tali da non essere distinguibili, che quindi
cadono
entrambe dentro la stessa banda critica.
In acustica si dicono fenomeni di prima specie (o primo ordine)
quelli provocati da suoni che cadono nella stessa banda critica.
È il tipico fenomeno che si sente quando uno o più strumenti si
accordano su un unico suono (battimento fra le fondamentali). In questo
caso, le due frequenze producono, all'interno della chiocciola, due
onde che interferiscono fra loro e formano il battimento.
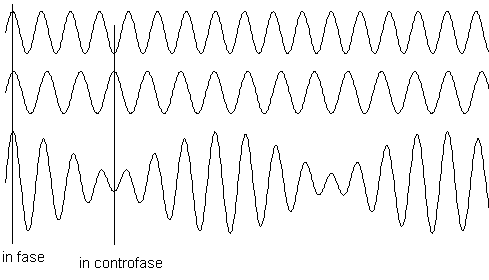
Il perché si formi è illustrato nella figura a fianco. Quando due onde
di frequenza leggermente diversa (sopra) iniziano, hanno probabilmente
la stessa fase, cioè si trovano entrambe nello stesso punto del ciclo.
In tal caso si rinforzano l'una con l'altra (si sommano) e il suono
risultante (sotto) avrà una ampiezza pari alla loro somma. Però, dato
che una frequenza è leggermente più alta dell'alta, il suo ciclo andrà
più veloce, quindi, dopo un po', le due onde saranno sfasate e a un
certo punto saranno in controfase, cioè il ciclo dell'una è nella parte
alta mentre quello dell'altra è nella parte bassa.
In questo caso, le due onde si annullano (si sommano algebricamente,
cioè si sottraggono) e il suono risultante sarà molto debole.
Il battimento, quindi, è una alternanza di fasi di rinforzo e
annullamento fra due onde di cui
questo
suono è l'esempio classico.
La frequenza del battimento, cioè la sua velocità, è determinata dalla
differenza in frequenza fra le due onde, mentre la frequenza del suono
effettivamente sentito è la loro media. Per esempio, se mettiamo
insieme un LA a 220 Hz e un LA a 222 Hz, sentiremo un LA a 221 Hz (la
media: (220+222)/2) con un battimento a 2 Hz (che si ripete 2 volte al
secondo).
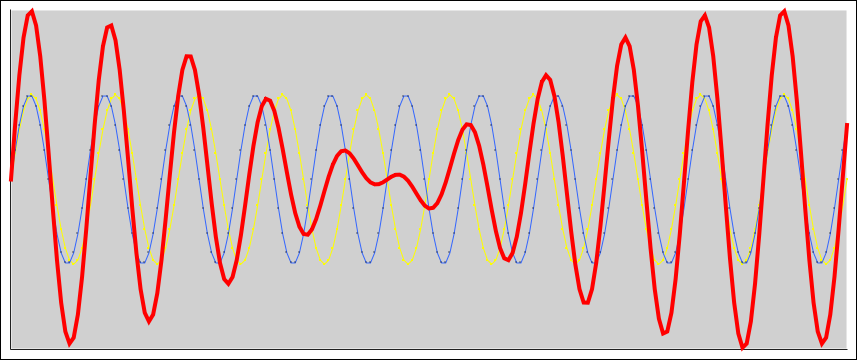
La figura sotto mostra le onde sovrapposte: in blu e giallo le onde che
creano il battimento, in rosso l'onda risultante dalla loro somma
algebrica.
Il battimento di prima specie è un fenomeno acustico e psicoacustico
che si può creare sia in aria, quando le onde provengono dallo stesso
punto, che nella chiocciola per interferenze fra le onde che si creano
nel liquido in essa contenuto.
Battimenti di seconda specie (o secondo ordine)
Ma, anche se sembra strano, si possono avere battimenti anche fra onde
fra loro lontane in frequenza. Sono i battimenti di seconda specie che
hanno origine neurologica, cioè sono provocati dalla elaborazione del
suono effettuata nel cervello.
In acustica si dicono fenomeni di seconda specie (o secondo ordine)
quelli provocati da suoni che non cadono nella stessa banda
critica per cui la loro origine non può essere attribuita a
interferenze nella chiocciola.
Ascoltate
questo esempio in cui un
battimento, seppure leggero, si sente chiaramente. Le due frequenze
sono di 220 e 445 Hz (8va leggermente stonata).
Ascoltate ora
questo esempio di
battimento binaurale, così chiamato perché il suono è stereo e le
onde che creano il battimento stanno una sul canale destro e l'altra
sul sinistro. Il punto è che questo battimento SI SENTE ANCHE IN CUFFIA
quando le onde non hanno alcun modo di interagire se non nel cervello.
In musica questo tipo di battimento si ha quando a interagire sono, per
es., la fondamentale e gli armonici.
Battimenti in musica
In musica, difficilmente esistono onde senza armonici, quindi si hanno
battimenti complessi, contemporaneamente di prima e seconda specie.
Ascoltate
questo esempio in cui
abbiamo 3 suoni che illustrano vari casi in cui ascoltiamo insieme i
battimenti di 1a specie fra le fondamentali e fra gli armonici uguali e
di 2a specie fra fondamentali e armoniche in 8va.
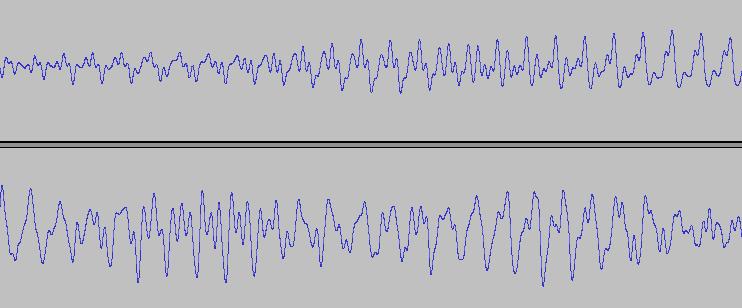
Si sente nettamente che vi sono vari battimenti insieme. Nella figura
seguente potete anche vedere le onde e rendervi conto della maggiore
complessità.

Toni di combinazione
Un altro effetto delle interferenze fra onde è quello dei cosiddetti
toni di combinazione, fra cui il più famoso è il terzo suono di Tartini
(che è anche quello che si sente più facilmente). Si tratta di suoni in
realtà non esistenti, prodotti da varie combinazioni di differenza fra
le frequenze dei due suoni generatori o fra le loro ottave.
Devo avvertirvi che i toni di combinazione sono un argomento
controverso. Se da un lato è evidente che, in certe condizioni, si
sentono, non tutti
gli studiosi sono d'accordo sia sulla loro origine (cervello o
chiocciola) sia sulle condizioni migliori per sentirli.
Il dato di
fatto è che anche il terzo suono (il più facile) non è sentito da tutti
e non si sente sempre. Si può sentire, per es., su un pianoforte e non
su un altro oppure, nel caso di registrazioni, con delle casse ma non
con altre e spesso anche la distanza dalle casse o dagli strumentisti è
importante. Quindi non preoccupatevi se non li sentite. Chiaramente, il
violinista che ha lo strumento a 10 cm dalla testa, con tutte le onde
che arrivano al suo orecchio sinistro, è nella condizione migliore per
sentirli (non
a caso se ne è accorto Tartini).
Il terzo suono
Il terzo suono di Tartini corrisponde alla differenza fra
le frequenze generatrici: un LA a 440 Hz e un MI 660 Hz,
quindi, producono un LA 220 Hz cioè l'8va sotto (660 - 440 = 220).
In
questo esempio è proprio così. Si
sentono le due frequenze generatrici a 440 e 660, prima staccate e poi
unite. Quando suonano insieme si avverte la presenza del LA 220 (terzo
suono) che poi è ripetuto da solo come
controprova. Qui nel mio studio, con i miei altoparlanti (ma anche in
aula) si sente l'8va sotto, sia pure debolmente. D'altra parte tonica e
dominante insieme hanno quella forza anche perché spesso si crea l'8va
inferiore.
Questo sistema è utilizzato anche nella costruzione degli
organi per creare un DO basso per cui sarebbe necessaria una canna
troppo lunga. A volte, al posto di questa canna se ne mettono due, una
al DO 8va sopra e una al SOL 12ma. Come nell'esempio appena sentito,
esse creano il DO basso.
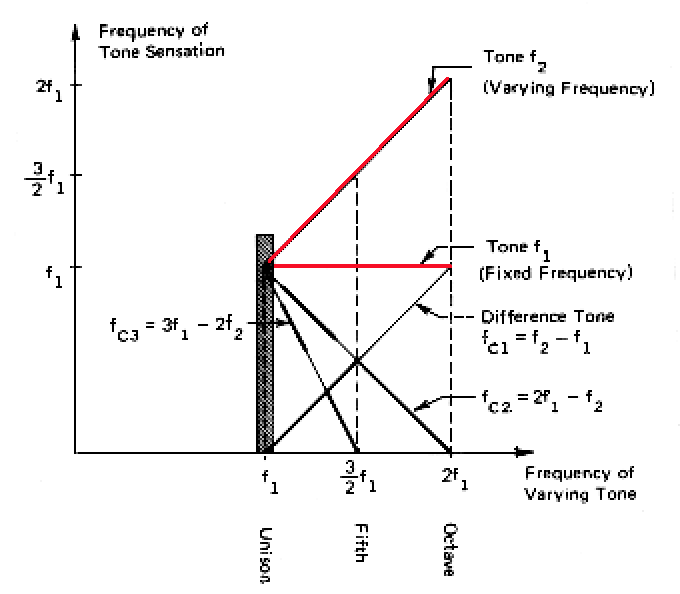
Lo specchio completo dei possibili toni di combinazione, però, non si
esaurisce con il terzo suono. Oltre a quest'ultimo, che è la differenza
semplice fra le frequenze generatrici (f
2 - f
1),
in teoria è possibile sentire anche un suono di frequenza pari a (2f
1
- f
2) e un altro pari a (3f
1 - 2f
2).
Bisogna però provare con coppie di frequenze diverse da tonica e 5a
perché in questo caso due toni di combinazione coincidono e il terzo è
zero. Infatti abbiamo:
660 - 440 = 220
2*440 - 660 = 220
3*440 - 2*660 = 0
In tutta sincerità, l'unico che sono certo di aver sentito è il terzo
suono. Gli altri... forse.
Comunque in
questo esempio audio
si sentono due frequenze di cui una è fissa, mentre l'altra glissa fino
all'8va sopra (in rosso in figura). Ascoltandolo con un buon impianto,
dopo i battimenti si sente un suono basso che glissa verso l'alto. È il
terzo suono (in figura è chiamato Difference Tone). Se qualcuno sente
anche gli altri toni di combinazione visibili in figura, me lo faccia
sapere.
La percezione delle altezze
Finiamo questo lungo capitolo con alcune considerazioni sui legami fra
l'altezza e gli altri parametri del suono.
La durata ha una certa influenza sull'altezza in quanto diventa
difficile giudicare l'altezza se il suono è di durata molto breve ed è
impossibile farlo se la durata è inferiore a 1/100 di secondo. Questo
perché il cervello ha bisogno di una durata minima per elaborare il
segnale.
In questo esempio sentite un suono
molto breve, la cui durata si accorcia ancora. Sentirete chiaramente
che a un certo punto non c'è più alcuna altezza e il suono diventa un
toc indistinto.
Anche la dinamica ha una certa influenza sul suono. Vari esperimenti
indicano che l'altezza stimata cambia un po' se il suono è più o meno
meno forte. Anche questa è una questione controversa. In questo esempio, il bicordo sembra
cambiare un po'.
Infine, una questione non controversa è che la sensazione di 8va si
espande andando sui suoni molto acuti e si stringe in quelli molto
gravi. Nella figura seguente si vede lo schema dell'accordatura di un
piano da concerto effettuata da due diversi accordatori. Dove la linea
coincide lo lo zero, è stato rispettato il sistema temperato. Dove
sale, gli intervalli sono espansi, mentre dove scende, sono ristretti.
La misura della deviazione è in cents, per si tratta di deviazioni
piccole, però, nella parte alta l'espansione massima supera di poco i
30 cents, mentre in quella bassa, arriva anche a 60 cents (più di 1/4
di tono).
Se ricordate, durante una lezione vi ho
fatto ascoltare questo esempio in cui
si ascoltano tre coppie di suoni di cui il primo è sempre 3000 Hz e il
secondo dovrebbe essere la sua 8va (quindi 6000), invitandovi a
indicare quale delle coppie fosse l'8va giusta. Quasi tutti (me
compreso) avete indicato la seconda o la terza che sono espanse. In
realtà l'8va giusta è la prima (3000 - 6000); la seconda è 3000 - 6500
(circa 9a min) e la terza è 3000 - 7000 (circa 9a magg).
Per ovviare a questo fenomeno, nel 1947 è stata proposta la scala in
Mel (figura sotto) che, rispetto agli Hertz, se espande molto sugli
acuti e si contrae un po' sui bassi (la scala è stata definita
sperimentalmente, non con una relazione matematica), che però non ha
trovato grande favore. Ecco la scala
cromatica in Mel.






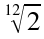 =
1.0594631 (approssimato)
=
1.0594631 (approssimato) Una scala cromatica, per noi, equivale a una
scala con gradini tutti uguali, praticamente una linea retta, come la
linea in rosso nella figura a destra.
Una scala cromatica, per noi, equivale a una
scala con gradini tutti uguali, praticamente una linea retta, come la
linea in rosso nella figura a destra.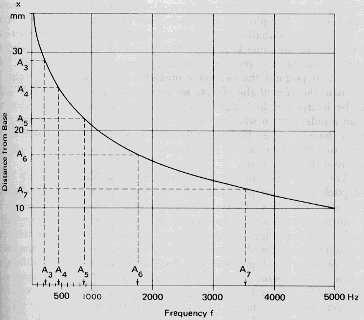


 Banda critica
Banda critica
 Ora vediamo un po' più in dettaglio alcuni
fenomeni legati alla banda critica.
Ora vediamo un po' più in dettaglio alcuni
fenomeni legati alla banda critica.


