Mauro Graziani - Dispense di Acustica per Musicisti
Acustica 06
Il Timbro
Un fenomeno multidimensionale
Il
timbro è un fenomeno multidimensionale
il che significa che il timbro, pur essendo considerato una
proprietà
del suono come l'altezza e la dinamica, non può essere espresso con
un
singolo numero in una qualche unità di misura. Non possiamo dire che
il
timbro di un suono è 25 qualcosa o 1100 qualcos'altro. Come vedremo,
misurare il timbro significa prendere in considerazione una certa
quantità di parametri.
La teoria classica: gli armonici
Alla metà dell'800 Helmholtz dimostrò in modo scientifico
l'esistenza
degli armonici, cosa che era già nota intuitivamente fin dai tempi
di
Rameau, formalizzando quella che è nota come la teoria classica del
timbro.
Secondo questa teoria, il timbro di un suono è determinato dai suoi
armonici. Ma cos'è un armonico?
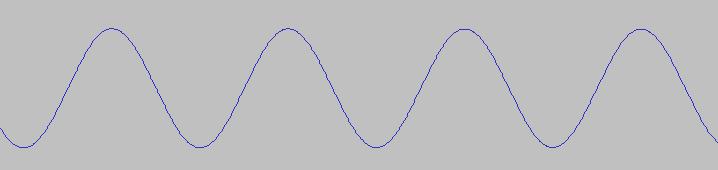
Ogni onda può essere scomposta in una serie di onde semplici e prive
di
armonici, dette sinusoidi (in figura), ognuna delle quali ha una
certa
frequenza, una certa ampiezza e una certa fase (ma quest'ultima ci
interessa meno delle altre due).
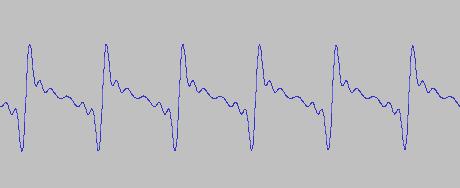
Consideriamo
questo
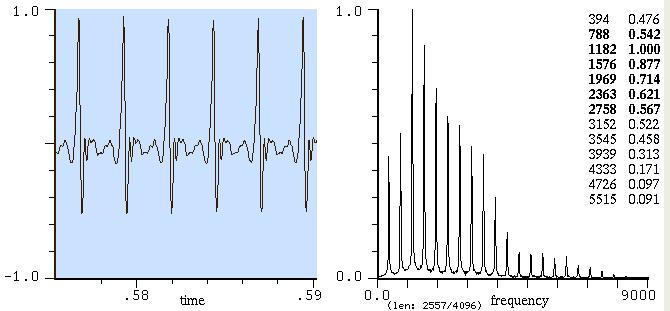
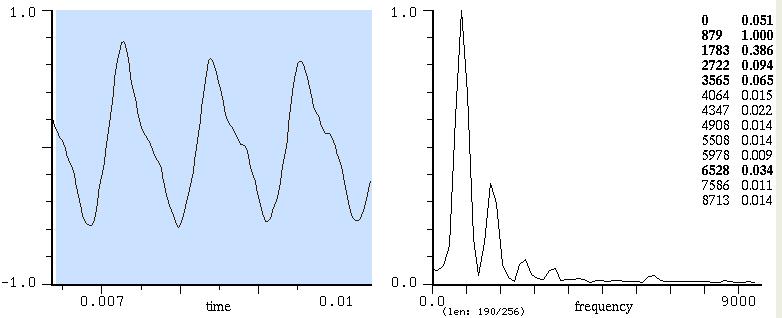
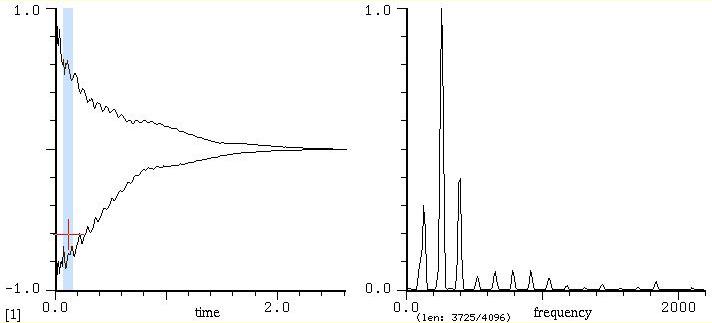
suono prodotto elettronicamente. Questa è la sua forma
d'onda
Quello che vedete sotto è il risultato della scomposizione e la sua
rappresentazione.
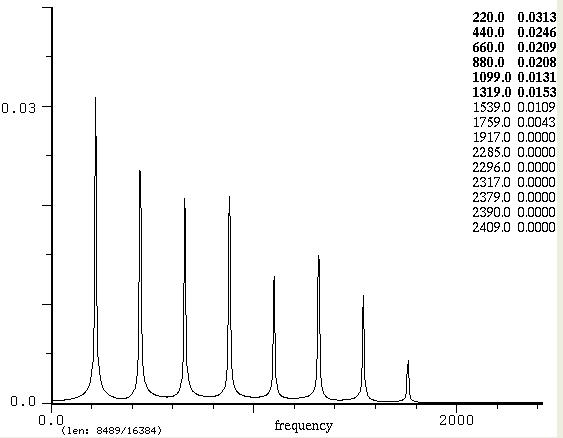
Quello che stiamo guardando è lo spettro del suono in esame.
Sull'asse orizzontale troviamo le frequenze, su quello verticale le
loro ampiezze.
Nell'immagine, ogni componente è piazzata al suo posto sull'asse
orizzontale delle frequenze e la sua ampiezza è rappresentata da una
linea verticale proporzionale al valore di ampiezza. I valori
numerici
di frequenza e ampiezza sono in alto a destra.
Vediamo che questo suono può essere visto come una sovrapposizione
di 8
sinusoidi la cui frequenza in Hz è il primo dei due numeri, mentre
il
secondo rappresenta l'ampiezza che qui non è in dB, ma in una scala
in
cui il valore 1.0000 rappresenta convenzionalmente la massima
ampiezza
possibile (non prendiamo in considerazione le sinusoidi con ampiezza
0.0000 o molto vicina: sono solo valori parassitari dovuti ai
calcoli.
In effetti, qualsiasi analisi deve essere interpretata e confrontata
con
l'ascolto).
Ma allora, se il suono che abbiamo
sentito è formato da queste 8 sinusoidi, sovrapponendole dovremmo
ottenere il suono di partenza? Naturalmente. In
questo esempio potete ascoltare le 8
sinusoidi prima in scala ascendente, poi in forma di arpeggio e
infine
perfettamente sovrapposte a formare il suono che abbiamo
analizzato.
A questo punto punto possiamo affermare che
ogni
suono può essere scomposto in una serie di sinusoidi con
relative
frequenze e ampiezze
e a partire da queste ultime può essere anche ricomposto.
Ma queste sinusoidi sono gli armonici? La risposta è non sempre. In
questo caso specifico, sì. Se osserviamo la serie delle frequenze
notiamo che
- la più bassa, che in questo caso è la fondamentale, è 220 Hz,
cioè un LA
- la frequenza delle altre sinusoidi è sempre un multiplo della
fondamentale (o quasi). 440=220*2; 660=220*3; 880=220*4; 1099
quasi = a
220*5 (sarebbe 1100); 1319 quasi = a 220*6 (sarebbe 1320).
Per questa ragione (frequenze multiple di quella della fondamentale)
in
questo caso le sinusoidi sono armonici. In realtà, la cosa deve
essere
generalizzata come segue
ogni
sinusoide in cui un suono è scomposto viene chiamata parziale (o
componente)
se
la frequenza di una parziale è multipla di quella della
fondamentale,
essa è una armonica
Ne consegue che una parziale può essere o non essere una armonica,
quindi esistono anche dei suoni le cui parziali non sono armoniche.
Sono quelli che la teoria classica chiamava "rumori" o "suoni non
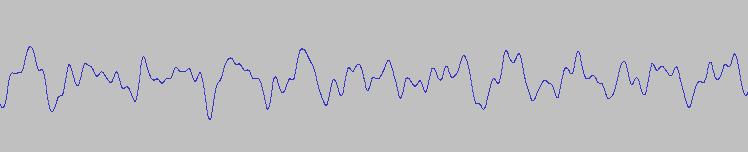
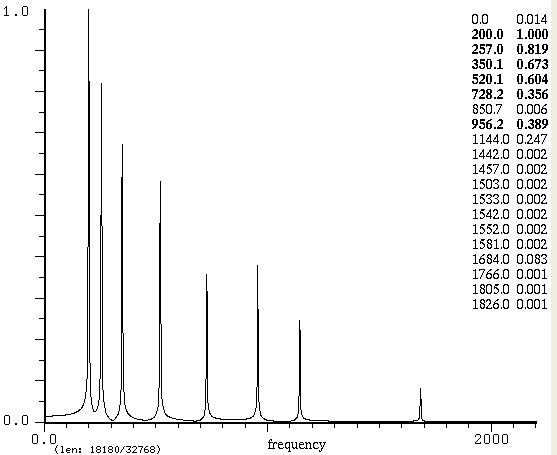
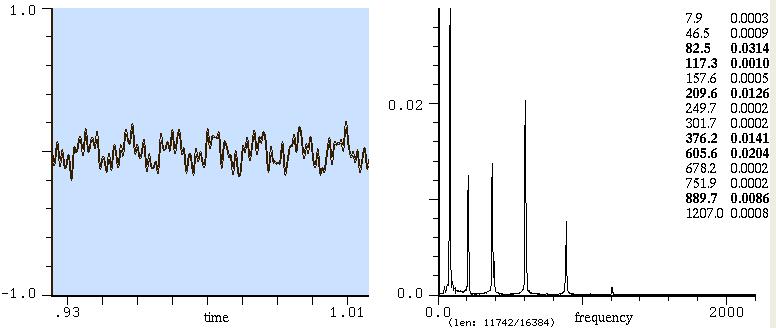
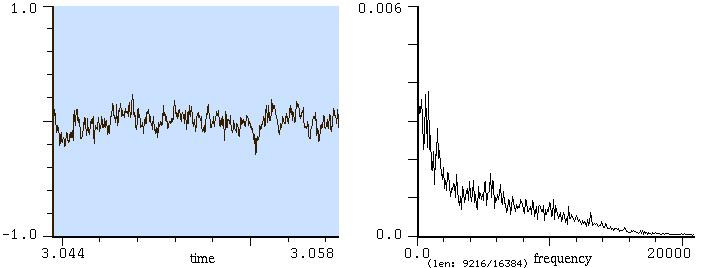
musicali", ma che oggi sono soltanto suoni. Ascoltate questo suono, vagamente simile a una
campana, di cui potete vedere la forma d'onda in figura
Ascoltandolo, vi serete accorti che
non
suona come una nota precisa, ma come una specie di accordo. Notate
che
la forma d'onda qui sopra non è periodica. Ora vediamo l'analisi
Qui la situazione è più complessa. La
componente più bassa (200 Hz) potrebbe essere una fondamentale, ma
nessuna delle altre è un multiplo di 200 (non ci vanno nemmeno
vicino).
Infatti, questo suono non ha componenti armoniche, ovvero ha
parziali
inarmoniche. La cosa è evidente anche confrontando i due grafici:
nel
primo le parziali hanno sempre la stessa distanza orizzontale,
segno
che fra loro c'è sempre la stessa distanza in frequenza; nel
secondo no.
Qui potete sentire le componenti di
questo suono in forma di scala, arpeggio e insieme. Notate come il
grado di fusione delle parziali in un unico suono non sia così forte
come del caso degli armonici.
Ora confrontate i due suoni che abbiamo analizzato
Suono
|
Onda
|
Parziali
|
Percezione
|
Il primo
|
Periodica
|
Armoniche
|
Nota
precisa (LA) |
Il secondo
|
Non
periodica
|
Inarmoniche |
No
nota precisa
|
Con una certa cautela, possiamo arrivare alle seguenti conclusioni
basate sulla forma d'onda
se
un'onda è chiaramente periodica, quasi certamente ha parziali
armoniche
se
un'onda non è periodica, quasi certamente ha delle parziali
inarmoniche
Perché, in entrambi i casi, non possiamo dare una certezza? Perché
in
natura esistono sempre dei casi particolari. Per esempio, molti
strumenti che suonano all'unisono non sono intonati perfettamente
sullo
stesso numero di Hertz (non è umano). Si crea quindi quel complesso
gioco di battimenti che è tipico di questa situazione. L'onda
potrebbe
avere una periodicità molto difficile da individuare, tuttavia,
all'ascolto, sentiremo una nota precisa.
Una situazione analoga si ha quando il suono ha un forte componente
di
rumore, come può essere in certi strumenti a fiato, oppure è formato
da
più suoni leggermente stonati, come nel pianoforte.
Inoltre, non basta esaminare la forma d'onda in un punto, ma bisogna
guardarla per tutto il corso della nota. Ora vedremo dei casi reali,
ma, innanzitutto, ascoltiamo
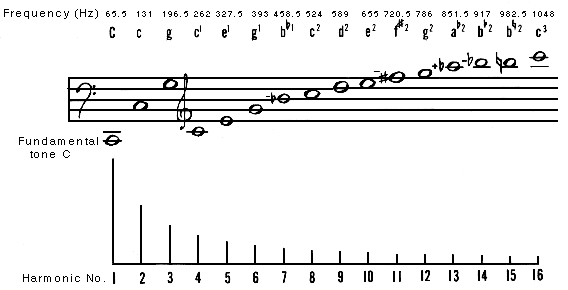
questa serie degli armonici (fino al 16mo) e vediamo a quali
note
corrispondono (ATTENZIONE: il DO iniziale è troppo basso per molti
altoparlanti da computer e essendo una sinusoide priva di armonici,
rischiate di non sentirlo).
Ascoltate ora questo
esempio
in cui gli armonici arrivano uno dopo l'altro sommandosi
(fondendosi)
insieme.
Analisi di suoni reali
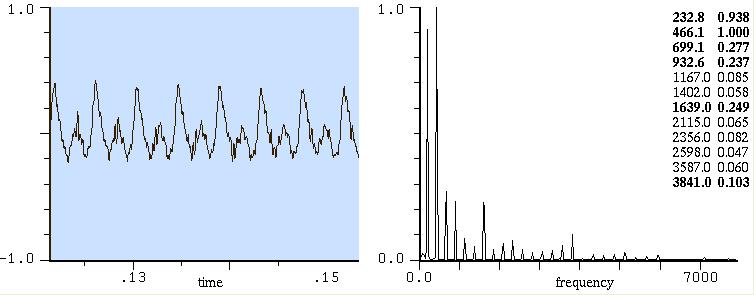
Subito un caso complesso. SIb di
pianoforte.
Notate l'alto numero di
parziali armoniche, sia pure con qualche piccola deviazione (la
fondamentale è 232.8). Notate
anche che la parziale che ha
maggior ampiezza è la seconda, all'8va sopra la fondamentale. Non è
un
caso particolare. Accade spesso e dipende dalla cassa di risonanza o
dalla risonanza del corpo dello strumento (ne parliamo più avanti).
Guardate sempre il numero in basso a destra, sotto l'asse
orizzontale
come riferimento per l'estensione dello spettro.
E ora qualche suono con parziali inarmoniche
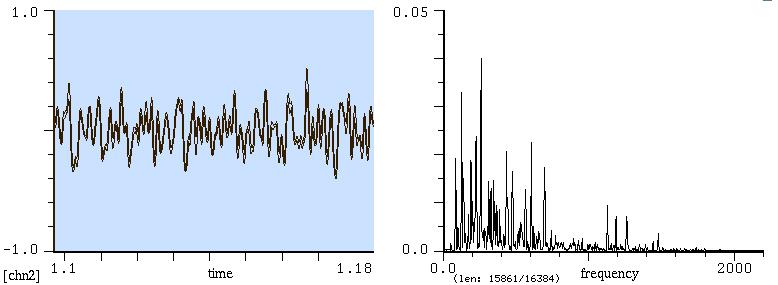
Un gong
Tam-tam (grande gong non
intonato)
Piatto (batteria)
Notate come, in questi ultimi due casi che si avvicinano molto al
rumore indifferenziato (soprattutto il piatto), non abbia più senso
parlare di parziali, ma solo di bande di rumore più o meno estese.
Nel
caso del piatto c'è una banda intorno ai 6000 Hz e un'altra fra i
12000
e 20000 Hz.
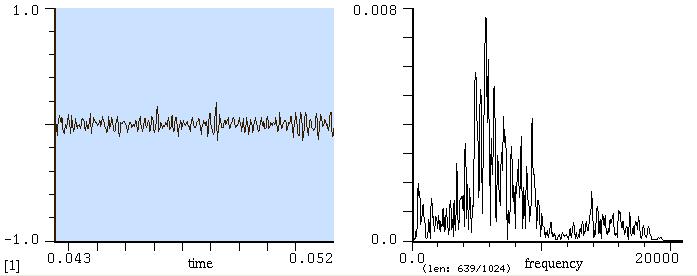
Ora guardate un rumore quasi totalmente indifferenziato come quello prodotto da una fontana
Come vedete, non si vedono parziali, ma solo una banda continua la
cui
ampiezza diminuisce verso gli acuti
I limiti della teoria classica
Secondo la teoria classica, il timbro di un suono è determinato
unicamente dalla forma d'onda e dalle sue parziali (armoniche o
inarmoniche). Se fosse vero, sarebbe molto facile ricreare in studio
un
suono reale. Basterebbe riprodurre la forma d'onda con il suo
contenuto
armonico.
Abbiamo già visto due casi (i primi due esempi) in cui questo
procedimento ha funzionato, ma, in realtà non funziona quasi mai.
Ecco
una prova: considerate questa nota di
pianoforte, di cui vedete lo spettro
Ora riproduciamo la forma d'onda inserendo le parziali armoniche
trovate con l'analisi, ognuna con la sua ampiezza, e diamo al suono
un
inviluppo simile a quello del pianoforte. Ne esce questo: un suono un po' simile,
ma
decisamente non uguale. Quindi la teoria non funziona. Cosa manca?
Il primo problema sta nel fatto che i suoni reali non sono fissi.
Nella
realtà l'ampiezza delle parziali non rimane fissa, ma cambia. Nelle
fasi di attacco e rilascio cambia notevolmente, ma anche nella fase
di
tenuta, in cui il suono sembra fisso, ci sono dei leggeri
cambiamenti.
Il pianoforte, poi, è uno strumento a evoluzione libera, privo di
una
fase di tenuta, quindi l'ampiezza delle parziali cambia sempre.
Il
suono è una cosa viva e si
evolve nel tempo.
In tutte le analisi che abbiamo visto, invece, la componente
temporale
non c'è mai. Si tratta di analisi istantanee che fotografano il
suono
in un particolare istante (un po' come una vostra foto a 5 anni:
siete
voi, ma non voi adesso).
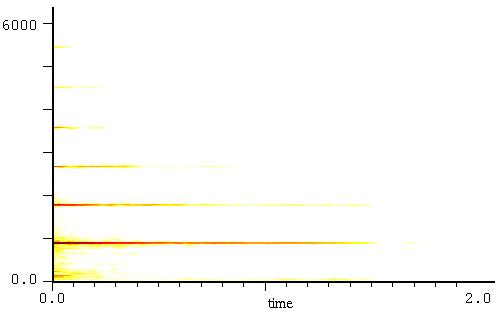
Guardate, invece, questo tipo di analisi. Qui abbiamo le frequenze
sull'asse verticale e il tempo su quello orizzontale. Le parziali
sono
le linee colorate e la loro ampiezza è rappresenta con il colore
(colore scuro = ampiezza elevata). Qui perdiamo un po' di
definizione
in ampiezza per vedere l'evoluzione temporale. Questo tipo di
grafico è
chiamato sonogramma.
Si vede benissimo che le parziali non hanno tutte la stessa durata.
Quelle più acute finiscono prima. Si tratta di una caratteristica
comune a tutti i mezzi vibranti che riescono a sostenere più
facilmente
le vibrazioni basse e lente rispetto a quelle acute e veloci.
Il segno in basso vicino a 0.0 con frequenza bassa e durata breve è
il
rumore del martelletto.
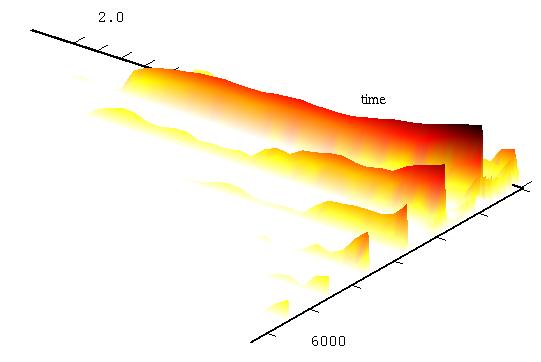
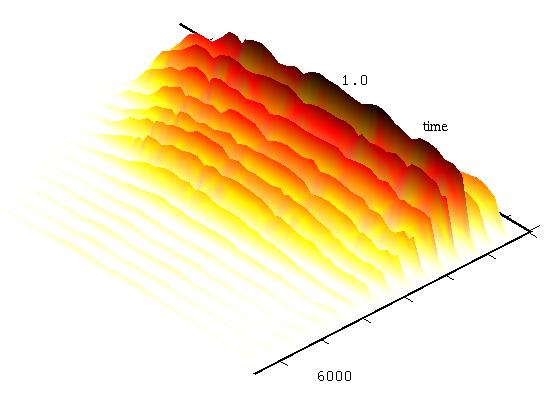
Ora guardiamo un altro bel grafico in cui il suono è
rappresentato come un paesaggio montagnoso.
Qui abbiamo frequenza e tempo sui due assi, mentre le ampiezze si
elevano in verticale. Si tratta di uno spettrogramma in cui possiamo
vedere l'inviluppo di ogni singola parziale. Da qui vediamo, per
es.,
che la durata delle tre armoniche più alte è molto breve rispetto
alle
altre. La collina vicina all'angolo degli assi è il rumore del
martelletto. Ovviamente nulla di tutto ciò sarebbe mai stato
possibile
senza la potenza di calcolo dei computer attuali.
Questo programma può anche salvare i dati per risintetizzare tutte
le
componenti e riprodurle. In questo
esempio, quindi, possiamo ascoltare le parziali della nota di
pianoforte senza il rumore dell'attacco (che non è riproducibile
mediante somma di parziali). In quest'altro
esempio abbiamo anche
aggiunto il rumore del martelletto (generato con altri sistemi) e il
suono è praticamente identico
all'originale.
Disponendo di questo tipo di analisi, è utile anche osservare lo
spettrogramma della tromba in cui si vede come, anche nella fase di
tenuta, le parziali non hanno mai una ampiezza veramente fissa, a
causa
del fatto che l'esecutore non è una macchina e la sua azione ha
sempre
delle piccole variazioni.
In conclusione, possiamo affermare che la teoria classica deve
essere
estesa e che nella creazione del timbro giocano un ruolo importante
i
seguenti parametri:
le
parziali presenti
la
loro evoluzione nel tempo
il
tipo di attacco
eventuali
altre sonorità significative
(rumore di attacco, soffio, etc)
Evoluzione temporale del suono: analisi nel tempo
Per esemplificare l'importanza dell'evoluzione temporale, ora
esamineremo i suoni già visti sopra mediante sonogramma per
osservare la
variazione dello spettro nel tempo. Il link ai suoni non è riportato
essendo lo stesso degli esempi di cui sopra.
La differenza è che finora abbiamo visto una sola "foto" per ogni
suono presa in un punto significativo. Ma i suoni evolvono nel
tempo, quindi qui utilizzeremo dei sonogrammi, cioè delle immagini
che hanno
- il tempo in ascissa (asse x)
- la frequenza espressa in Hz in ordinata (asse y)
In tal modo ogni componente diventa una linea orizzontale in cui
l'ampiezza è espressa con un colore. In genere, tanto più il colore
è contrastato rispetto allo sfondo, tanto più alta è l'ampiezza (es:
sfondo bianco, max amp nero o viceversa), mentre colori vicini allo
sfondo sono indicatori di bassa ampiezza.
In questi esempi lo sfondo è bianco, quindi la scala delle ampiezze,
dal basso verso l'alto è:
giallo pallido - giallo -
arancione - rosso - marrone - nero
low amp --------------------------------------------
high amp
Guardando i sonogrammi, inoltre, è necessario porre attenzione al
valore massimo dell'asse x, che indica la durata, ma soprattutto al
valore massimo dell'asse y che indica l'estensione della banda a cui
arrivano le componenti del suono.
Ogni sonogramma racconta una storia che in qualche caso diventa un
romanzo. Bisogna saper leggere i sonogrammi come carta stampata.
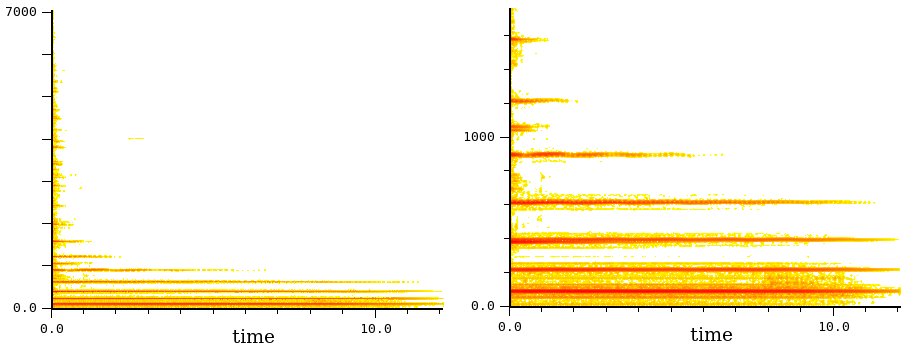
Sib di pianoforte
Notate:
- il rumore della percussione (martelletto) che si vede come
banda
rossa nel primo decimo di secondo. È un rumore indifferenziato
che si
estende ad alto volume fino a circa 7000 Hz, ma arriva anche più
in
alto.
- la grande quantità di armonici nella prima parte del suono.
All'istante dell'attacco si arriva fino a circa 15000 Hz
(qualcuno
isolato anche oltre)
- la rapida scomparsa delle componenti alte: la maggior parte è
già
sparita entro il primo secondo di suono. La loro durata decresce
in
funzione dell'altezza seguendo una curva esponenziale
decrescente. Questo
comportamento è tipico dei suoni a
evoluzione libera (pizzicati, percussivi).
- le componenti che vanno e vengono (linee interrotte), indice
di
battimenti
- il blob rosso finale sui bassi è lo smorzatore.
Sol basso di violoncello
Anche qui molti armonici, ma la
maggior parte è piuttosto debole. Solo quelli in rosso hanno una
ampiezza chiaramente sensibile, ma tutti gli altri, sebbene
singolarmente non siano così evidenti, nel loro insieme danno corpo
al
suono.
Le macchie in alta frequenza sono interpretabili (a posteriori) come
il
rumore dell'arco che è proprio uno sfregamento a frequenze alte.
Notate che, al momento dell'attacco, gli armonici arrivano quasi
tutti
insieme (con un beve ritardo), poi rimangono in buona parte stabili
per
tutta la durata del suono e scompaiono in breve tempo (a cominciare
dalle componenti alte) alla fine. Questo
comportamento
è tipico dei suoni a evoluzione controllata (archi,
fiati). In questo caso il decadimento è lungo (quasi 1/2 secondo) e
dipende dal fatto che la corda riesce ancora a vibrare se l'arco
viene
tolto di colpo.
In entrambi questi esempi abbiamo visto molti armonici. Ciò dipende
dal
fatto che, in entrambi i casi, abbiamo analizzato note basse
generate
da corde grosse. In genere, i suoni bassi hanno una maggiore
quantità
di armonici, per varie ragioni:
- le strutture vibranti più massicce possono vibrare in modo più
complesso rispetto a quelle sottili
- normalmente, le strutture vibranti che emettono suoni bassi
vengono trattate con maggiore violenza, sia perché sono più
massicce,
ma soprattutto per compensare l'effetto Fletcher (vedi Dinamica:
curve di Fletcher) per cui occorre una ampiezza assoluta
notevolmente
maggiore per produrre suoni percepiti allo stesso volume di
quelli
nella banda 500 - 2000 Hz
- gli armonici di fondamentali alte escono molto prima dalla
banda
udibile: una fondamentale a 100 Hz ha il 200mo armonico a 20000
Hz,
mentre se la fondamentale è a 2000 Hz, già il 10mo armonico è a
20000
Hz.
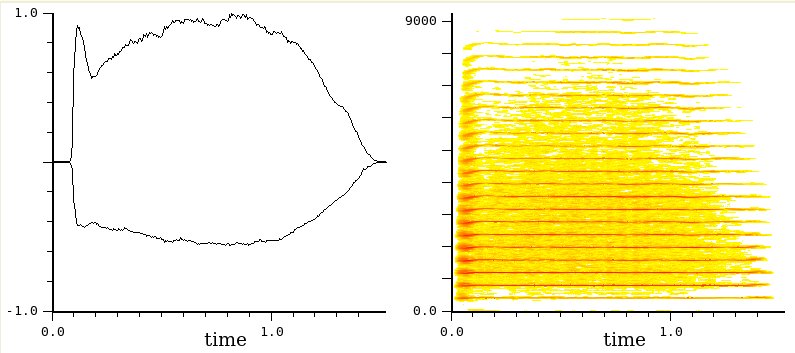
Sol di tromba
Due grafici per la tromba: a sin.
l'inviluppo, a des. il sonogramma.
Notate come l'attacco in sfz,
tipico degli ottoni e ben visibile nell'inviluppo (occorre superare
una
certa soglia perché scatti la vibrazione) si rifletta nel sonogramma
con componenti che all'inizio risultano più forti e meno precise (un
po' più sporche).
Notate anche come esista un leggero glissando al momento
dell'attacco,
più visibile nelle frequenze alte. In realtà l'entità del glissando
è
uguale, in percentuale, su tutte le componenti, ma, essendo l'asse Y
lineare e non logaritmica, si vede di più sugli alti (se è dell'1%,
a
300 Hz è 3 e a 3000 Hz è 30).
Infine, il giallo diffuso, è il rumore del soffio.
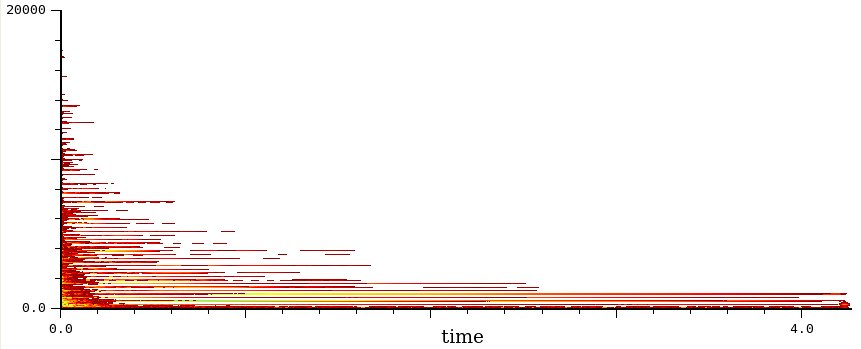
Gong
Un suono inarmonico, come si vede bene nell'ingrandimento a des. (la
distanza fra le componenti è variabile).
Per il resto, il quadro è quello tipico dei suoni a evoluzione
libera:
percussione iniziale con parecchie componenti che scompaiono
rapidamente seguendo un pronunciato andamento esponenziale.
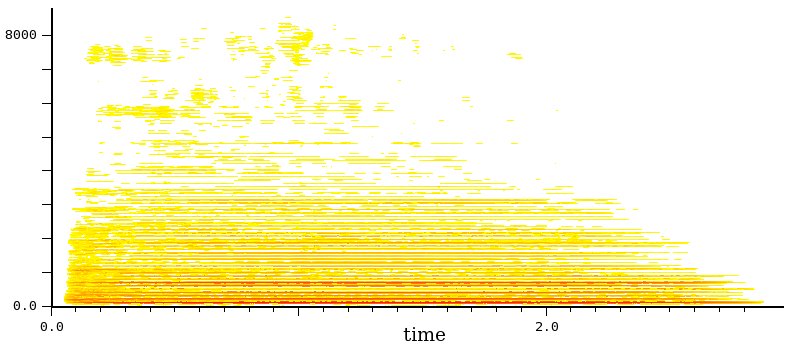
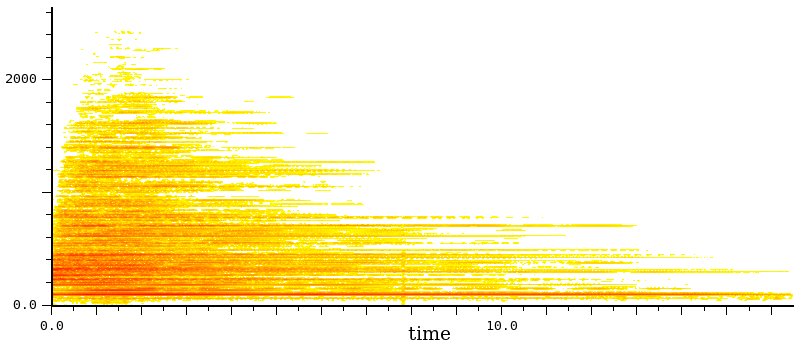
Tamtam
Molte componenti che vanno a riempire
dapprima lo spazio sui bassi e poi si estendono verso l'alto (il
tamtam
è grande e impiega tempo, circa 1 sec., a entrare in vibrazione
nella
sua interezza). Ci avviciniamo al rumore indistinto a banda
limitata,
ma esistono alcune componenti molto pronunciate (soprattutto quella
più
bassa che agisce come pseudo-fondamentale).
Il decadimento rispetta sempre la legge secondo cui gli alti se
vanno
prima, ma in modo meno regolare, a causa delle grandi dimensioni e
della diversa densità e spessore del materiale che lo compone.
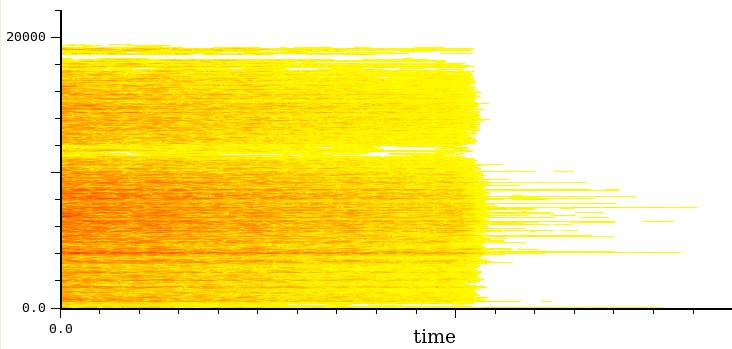
Piatto
Siamo al rumore indistinto. La
differenziazione fra le singole componenti si perde in favore di 2
bande: la prima arriva fino a circa 11000 Hz con centro intorno ai
6000/8000, la seconda fra 12000 e quasi 20000 Hz. Alcune componenti
della prima banda rimangono come rumore residuo (molto debole)
quando
il piatto è stoppato.
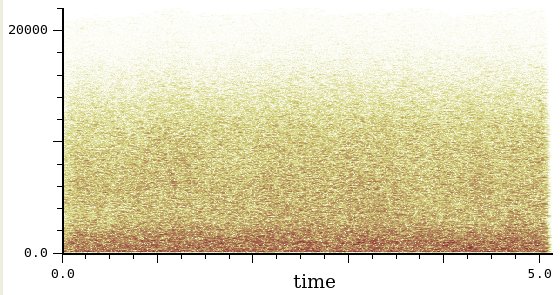
Fontana
Infine, la fontana: rumore statico,
indifferenziato, con maggior peso sulle frequenze basse. Notate la
differenza qualitativa con l'esempio precedente: qui non c'è il minimo accenno a delle
righe
che possano suggerire delle componenti.
La teoria formantica: lo strumento
In uno strumento musicale esistono sempre
- un elemento vibrante (quello che genera la vibrazione; è
chiamato eccitatore)
- un elemento risonante (che entra in vibrazione a causa
della
presenza del primo; è detto risuonatore)
L'esempio tipico è corda e cassa armonica, ma l'idea su può
estendere
anche a colonna d'aria e corpo dello strumento. Questi due elementi
formano il suono che sentiamo interagendo fra loro. Qual'è
esattamente
il
loro ruolo?
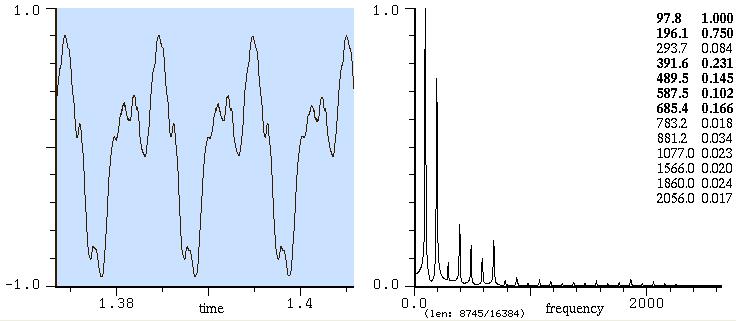
Osservate questa analisi di un suono di chitarra effettuata nel
punto
segnato in azzurro, cioè poco dopo l'attacco
Ora, noi sappiamo che una corda
vibrante, da sola, produce la fondamentale seguita da una serie di
armonici con ampiezza calante. Allora ci si può chiedere perché
qui la
seconda e la terza parziale sono entrambe più forti della
fondamentale?
E perché anche le parziali seguenti non hanno ampiezza
regolarmente
discendenti?
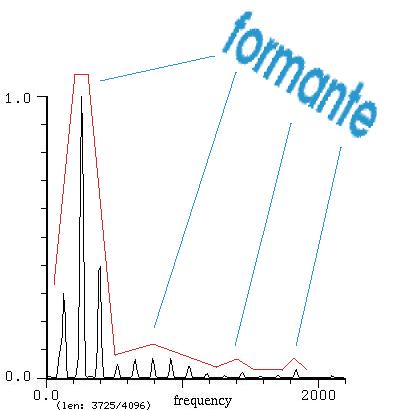
Tecnicamente, si dice che questo spettro mostra dei formanti.
formante
= concentrazione di energia acustica in una certa banda
frequenziale
Ne consegue che le parziali che si trovano entro quella banda hanno
una
ampiezza maggiore del normale. In figura vedete i formanti in questo
spettro di chitarra.
Qui, i formanti sono causati dalla cassa armonica, essenzialmente
per
due ragioni.
La prima (e principale) è che il materiale di cui è composta ha
delle
frequenze di risonanza, cioè vibra meglio in certe zone di frequenza
rispetto ad altre e il risultato è che le frequenze che si
trovano
in queste zone vengono rinforzate, mentre quelle che si trovano al
di
fuori vengono attenuate.
La seconda è che, nello spazio all'interno della cassa, le onde
sonore
prodotte dalla corda continuano a rimbalzare e si sommano alle onde
principali con un piccolo ritardo sufficiente, però, a mettere
certe frequenze in fase e altre in controfase (ricordate la
prima
figura sui battimenti), ancora con l'effetto di rinforzarne alcune e
attenuarne altre. Proprio per questa ragione non si costruiscono
casse
armoniche rettangolari, che sarebbero molto più facili da fare.
L'effetto di una forma così regolare sarebbe quello di creare una
serie
di rimbalzi regolari e quindi di amplificare troppo le frequenze il
cui
periodo è pari o multiplo al tempo di rimbalzo.
In pratica, la cassa armonica amplifica certamente il suono, ma non
agisce nello stesso modo su tutte le frequenze. Alcune sono
amplificate
maggiormente, altre vengono attenuate. In pratica
la
cassa armonica è un filtro che con la sua azione crea i formanti
che non devono essere visti come una cosa negativa perché
caratterizzano timbricamente il suono di tutto lo strumento.
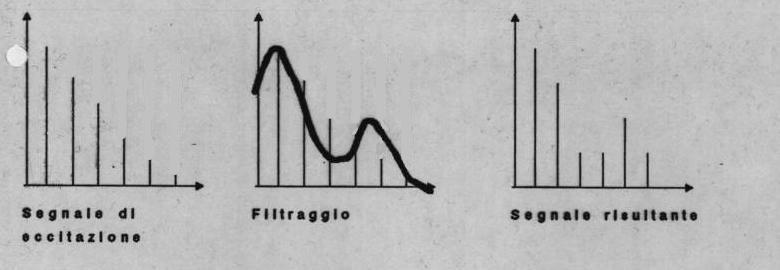
Quello che accade, in sintesi, è schematizzato in figura. La corda
fornisce un segnale con armoniche di ampiezza calante. Questo
segnale
viene rimodellato in base alle frequenze di risonanza della cassa
armonica che agisce da filtro. Il segnale risultante è il prodotto
dell'interazione di questi due elementi.
Questo fenomeno ha un importante effetto collaterale. La cassa
armonica
è fissa. Non cambia da una nota all'altra e nello stesso modo, sono
fisse le sue frequenze di risonanza. Quindi anche i formanti che
essa
crea sono sempre negli stessi punti, qualsiasi nota si faccia. Ora,
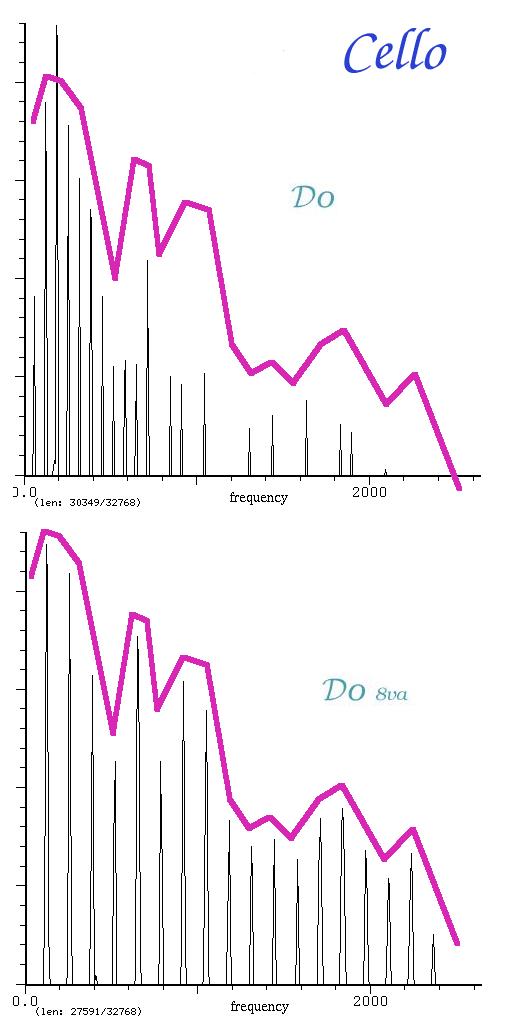
osservate questi due spettri di violoncello relativi a due note a
distanza di 8va.
Se osservate lo spettro del DO in 8va, il secondo, noterete che
nell'area del primo formante cadono la prima e la seconda parziale
(fondamentale e primo armonico). In questa nota la fondamentale è la
componente più forte.
Se ora guardate il DO più basso (il primo), noterete che, essendo
una
8va sotto e essendo il formante fisso, a cadere nella sua area qui
sono
la seconda e la terza parziale. Di conseguenza, qui non è la
fondamentale, ma la terza parziale a essere la componente più forte.
Il
che significa che, in un singolo strumento, il timbro cambia, sia
pure
gradualmente, da una nota all'altra.
La cosa non si verifica solo negli strumenti con cassa armonica. Qui potete vedere alcune analisi
di
note di tromba e constatare come cambia lo spettro su varie note.
Non esistendo una cassa armonica, i formanti della tromba sono meno
complessi di quelli degli strumenti con cassa, ma esistono e sono
dovuti alla risonanza della campana e del corpo dello strumento.
Probabilmente è proprio questo cambiamento timbrico provocato dai
formanti ad aver generato la nozione di "registro". Si dice, infatti
che lo strumento entra in un altro registro quando il cambiamento
timbrico diventa avvertibile.
Qui trovate i grafici dei
formanti
di vari strumenti basati su analisi dell'Università di Stanford.
Il principale strumento che si basa sui formanti resta comunque la
voce. La differenza fra le vocali, infatti, è legata unicamente alla
posizione dei formanti che viene modificata dalle diverse posizioni
che
può assumere il tratto vocale (i dettagli vanno oltre il programma
di
Storia della Musica, ma gli studenti curiosi possono trovarli in una
delle lezioni successive).
Sulle scoperte relative ai formanti si basa la teoria formantica del
timbro secondo la quale il nostro sistema percettivo riesce a
riconoscere la posizione dei formanti e proprio in base a questi
ultimi
è in grado di identificare lo strumento anche se in realtà lo
spettro
cambia di nota in nota.
Parlando della banda critica, abbiamo visto come la chiocciola sia
come
un analizzatore basato appunto sull'ampiezza di banda critica (circa
1/3 di 8va). L'intero campo udibile può essere diviso in 25 bande,
per
la maggior parte a terzi di 8va, e quindi il sistema percettivo è in
grado di misurare l'energia acustica presente in ogni banda. In
questo
modo i formanti possono essere identificati facilmente.
Si può quindi affermare che anche
la
posizione dei formanti gioca un ruolo importante nel
riconoscimento del
timbro