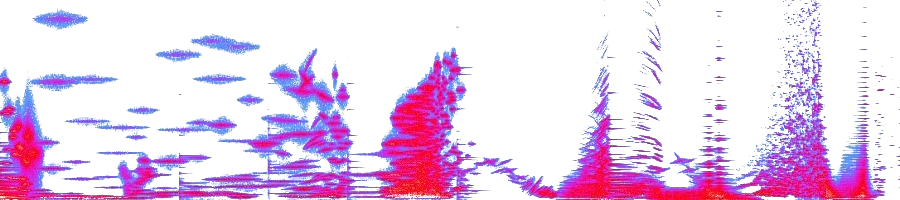
Tanto per fare un confronto al volo, ecco il procedimento di cui al post precedente con la serie di partenza basata su π, φ ed e.
Le altezze sono comprese fra C3 e C5 mentre le durate vanno da semicroma a minima.
Archivi categoria: Musica
Matematica e musica (01)
La trasposizione diretta della matematica in musica, di solito produce dei risultati abbastanza banali. C’è però qualche eccezione. Una è questa.
- Si calcolano le prime n (poniamo 100) cifre di un numero trascendente, uno di quei numeri non riducibili a frazione che hanno infinite cifre dopo la virgola, come π (pi-greco), φ (phi, la sezione aurea) o e (la base dei logaritmi naturali).
In questo caso, usiamo la sezione aurea φ (phi). Il risultato è
1.61803398874989484820458683436563811772030917980576
286213544862270526046281890244970720720418939113748 - Si prendono le cifre così come sono, senza badare al punto decimale, cioè
1,6,1,8,0,3,3,9,8,8,7,4,9,8,9,4,8,4,8,2,0,4,5,8,6,8,3,4,3,6,5, … etc.
Questa sarà la nostra base per produrre altezze e durate. L’idea è che la generazione delle cifre decimali in questi numeri non è del tutto casuale. Infatti le cifre non hanno la stessa distribuzione, ma soprattutto la serie è ricca di ripetizioni, configurazioni ripetute, etc. - Per ottenere le altezze, trasformiamo le nostre cifre in note con una codifica. Poniamo 1 = LA basso del piano e saliamo per semitoni. Quindi il DO più basso sarà 4 e poi, per ottave, gli altri DO saranno 16, 28, 40, 52, 64, 76, 88.
- Ora, riscaliamo l’intera serie, che va da 0 a 9, in modo che il minimo (0) corrisponda a 40 (C3) e il massimo (9) a 64 (C5). Otteniamo seguente serie di note:
42,56,42,61,40,48,48,64,61,61,58,50,64,61,64,50,61,50,61,45,40, … etc
In generale, risulta che- 0 = 40 = C3
- 1 = 42 = D3
- 2 = 45 = F3
- 3 = 48 = G#3
- 4 = 50 = A#3
- 5 = 53 = C#4
- 6 = 56 = E4
- 7 = 58 = F#4
- 8 = 61 = A4
- 9 = 64 = C5
Naturalmente avremmo potuto usare anche un altro intervallo, più o meno ampio di 2 ottave ottenendo risultati diversi.
- Ora piazziamo le durate. Decidiamo che
- 0 = semicroma
- 1 = croma
- 2 = semiminima
- 3 = minima
e riscaliamo la serie numerica come sopra, ma restringendola fra 0 e 3 senza decimali. Ne consegue che
- 0, 1, 2 = 0 = semicroma
- 3, 4, 5 = 1 = croma
- 6, 7, 8 = 2 = semiminima
- 9 = 3 = minima
ottenendo la serie seguente: 0,2,0,2,0,1,1,3,2,2,2,1,3,2,3,1,2,1,2, … etc.
In questo esempio usiamo sempre durate canoniche (non irregolari) per non avere difficoltà di scrittura. Niente però impedisce di usare anche durate irregolari, affrontando qualche problema di scrittura. P.es, usando anche la durata di una croma terzinata, potreste trovarvi una successione come: semiminima – croma terzinata – semiminima e voglio vedere come lo scrivete. Oddio, in tanti brani contemporanei si fa anche di peggio, ma in questo esempio stiamo sul semplice. - Bene. A questo punto abbiamo una serie di altezze e una di durate di pari lunghezza. Decidiamo un metronomo e suoniamo. Ecco il risultato finale. Simpatico, nervosetto, un po’ alla Xenakis anche se meno complesso.
Al lettore attento non sarà sfuggita una particolarità. Usando la stessa serie di partenza per altezze e durate, la durata aumenta via via che le altezze si alzano. Per evitarlo, basta retrogradare una delle due serie risultanti. In questo esempio abbiamo retrogradato le durate.
Cambiando l’estensione, poi i risultati sono diversi. Qui le altezze sono riscalate fra 4 e 64 usando buona parte dell’estensione del piano e rendendolo praticamente insuonabile da un umano a questa velocità.
Ecco infine una sovrapposizione di quest’ultimo frammento (1-64) e del precedente (40-64 con durate in retrogrado)
Myanmar
Un pensiero per la Birmania.
Uno dei brani più famosi della musica classica birmana. Anticamente veniva eseguito a palazzo reale e nelle occasioni in cui il re si rivolgeva al popolo.
E mentre ascoltate leggetevi
Rudyard Kipling, Mandalay
che avrà anche degli accenti un po’ da romantico colonialismo d’altri tempi e a tratti è buffa, però ha rappresentato per molto tempo la Birmania nell’immaginario occidentale…
By the old Moulmein Pagoda, lookin’ eastward to the sea,
There’s a Burma girl a-settin’, and I know she thinks o’ me;
For the wind is in the palm-trees, and the temple-bells they say:
“Come you back, you British soldier; come you back to Mandalay!”
Come you back to Mandalay,
Where the old Flotilla lay:
Can’t you ‘ear their paddles chunkin’ from Rangoon to Mandalay?
On the road to Mandalay,
Where the flyin’-fishes play,
An’ the dawn comes up like thunder outer China ‘crost the Bay!
‘Er petticoat was yaller an’ ‘er little cap was green,
An’ ‘er name was Supi-yaw-lat — jes’ the same as Theebaw’s Queen,
An’ I seed her first a-smokin’ of a whackin’ white cheroot,
An’ a-wastin’ Christian kisses on an ‘eathen idol’s foot:
Bloomin’ idol made o’mud —
Wot they called the Great Gawd Budd —
Plucky lot she cared for idols when I kissed ‘er where she stud!
On the road to Mandalay . . .
When the mist was on the rice-fields an’ the sun was droppin’ slow,
She’d git ‘er little banjo an’ she’d sing “Kulla-lo-lo!”
With ‘er arm upon my shoulder an’ ‘er cheek agin’ my cheek
We useter watch the steamers an’ the hathis pilin’ teak.
Elephints a-pilin’ teak
In the sludgy, squdgy creek,
Where the silence ‘ung that ‘eavy you was ‘arf afraid to speak!
On the road to Mandalay . . .
But that’s all shove be’ind me — long ago an’ fur away,
An’ there ain’t no ‘busses runnin’ from the Bank to Mandalay;
An’ I’m learnin’ ‘ere in London what the ten-year soldier tells:
“If you’ve ‘eard the East a-callin’, you won’t never ‘eed naught else.”
No! you won’t ‘eed nothin’ else
But them spicy garlic smells,
An’ the sunshine an’ the palm-trees an’ the tinkly temple-bells;
On the road to Mandalay . . .
I am sick o’ wastin’ leather on these gritty pavin’-stones,
An’ the blasted Henglish drizzle wakes the fever in my bones;
Tho’ I walks with fifty ‘ousemaids outer Chelsea to the Strand,
An’ they talks a lot o’ lovin’, but wot do they understand?
Beefy face an’ grubby ‘and —
Law! wot do they understand?
I’ve a neater, sweeter maiden in a cleaner, greener land!
On the road to Mandalay . . .
Ship me somewheres east of Suez, where the best is like the worst,
Where there aren’t no Ten Commandments an’ a man can raise a thirst;
For the temple-bells are callin’, an’ it’s there that I would be —
By the old Moulmein Pagoda, looking lazy at the sea;
On the road to Mandalay,
Where the old Flotilla lay,
With our sick beneath the awnings when we went to Mandalay!
On the road to Mandalay,
Where the flyin’-fishes play,
An’ the dawn comes up like thunder outer China ‘crost the Bay!
Robot Drum
I giapponesi, nella loro ossessione per i robot, non trascurano la musica.
Qui vedete alcuni robot impegnati al tamburo tradizionale daiko.
Quello che fanno può sembrare banale, ma non lo è. Se uno dei due esegue un ritmo regolare, l’altro suona in controtempo, il che significa che il secondo ascolta il primo e trattandosi di robot, non è poco.
La funzione della musica
the function of music is to comfort the disturbed and to disturb the comfortable
from Renewable Music
UPDATE
In verità ho postato questa definizione solo perché la trovo curiosa in quanto dà luogo a una reductio ad infinitum e mi chiedo se l’inventore (che non so chi sia) o qualche lettore se ne sia reso conto.
Infatti, secondo la definizione, se qualcuno è disturbato (disturbed), la musica lo rimette a suo agio (comfortable). Ma a questo punto, essendo a proprio agio, la musica lo dovrebbe disturbare, e così via…
Cattiverie (1)
Questa fin’adesso non l’avevo mai raccontata perché non è proprio politically correct, comunque adesso ho le p…e girate e la metto.
Dunque, siamo negli USA e c’è Bocelli che canta in TV.
Lui e lei si stringono commossi davanti allo schermo e lui dice: “Però, come canta bene Pavarotti…”
E lei fa: “Sì, ma deve aver fatto una dieta; guarda com’è dimagrito…”
Lui: “È vero. Ma non deve avergli fatto bene: sembra orbo…”
Non sono i primi
Igudesman & Joo non sono i primi a farci ridere con i classici. Guardatevi Dudley Moore, nei primi anni ’60, mentre si lancia in una parodia della sonata beethoveniana usando il tema del Ponte sul Fiume Kwai.
In this clip from the 1950’s-60s British comedy group “Beyond the Fringe,” Dudley Moore plays a very funny but also very musically well-done parody of a Beethoven Piano Sonata, using the famous whistling tune from “Bridge Over the River Kwai” as a thematic subject.
The Julliard Manuscript Collection

La Julliard School ha messo in internet la propria collezione di partiture manoscritte. Da Bach a Mozart, a Beethoven, attraverso i romantici fino a Debussy, Stravinsky, Malipiero, Britten e vari altri.
Il sito funziona molto bene ed è possibile zoomare sul testo fino ai minimi dettagli.
The Julliard Manuscript Collection è qui.
Nell’immagine Debussy
La prima macchina musicale (forse)

L’idea di costruire una macchina in grado di riprodurre la musica è sempre esistita.
La prima macchina “musicale” di cui abbiamo notizia è la colossale statua di Memnone a Tebe, costruita intorno al 1500 AC. In realtà si tratta di due statue gemelle che rappresentano il faraone Amenhotep III (XV secolo AC) in posizione seduta, con le mani sulle ginocchia e lo sguardo rivolto a est, verso il fiume e il sole nascente. Solo una di esse, però, era sonora.
Il nome con cui sono tuttora conosciute queste statue, Colossi di Memnone, fu coniato dagli storici greci, che le associarono all’eroe mitologico.
Memnone, infatti, è un personaggio omerico: re etiope, figlio dell’Aurora e di un principe troiano, accorse in aiuto di Troia e perì sotto le sue mura per mano di Achille.
Nell’immaginazione dei visitatori di età classica, l’eroe raffigurato nella statua salutava la madre (Eos dea dell’alba) con un suono come di corde di cetra che si spezzassero. La cosa è stata spiegata con la presenza, nella quarzite in cui è intagliata la statua, di cristalli, i quali in un certo qual modo si assestavano in seguito alla differenza di temperatura, veramente notevole in quella zona, tra la notte ed il giorno. [ipotesi del prof. Barocas].
Dopo un restauro, effettuato in epoca romana per volere dell’imperatore Settimio Severo, nel 199 d.C. i suoni cessarono di essere udibili.
tratto dalla mia dispensa dedicata alla Cronologia della Tecnologia Audio e della Musica Elettroacustica.
…Amo l’immensa superficie del silenzio
If music were to assume human form and explain its essence, it may say something like this: “…I love the vast surface of silence; and it is my chief delight to break it.”
Se la musica potesse assumere forma umana e spiegare la propria essenza, direbbe qualcosa come: “…Amo l’immensa superficie del silenzio; e il mio principale piacere consiste nell’interromperla”. [trad. mia]
Carl Nielsen (1865-1931), compositore danese
from The Rest is Noise
La citazione, tratta dal blog di Alex Ross, è molto bella e poetica, ma io non la condivido. È inconsistente. Sono solo belle parole messe in fila.
Prima di tutto perché ripropone l’antica contrapposizione fra suono e silenzio, che Cage ha mostrato essere illusoria.
Finché c’è un mezzo che trasporta il suono, il silenzio, infatti, non esiste. Cage racconta la parabola della camera anecoica nella quale, chiuso in una stanza ermetica al suono, egli cominciò a sentire i suoni prodotti all’interno del proprio corpo: il basso hum della circolazione sanguigna e il beep del sistema nervoso.
Allora qualcuno ha tentato di risolvere l’impasse affermando che dove c’è vita c’è suono, ma nemmeno questo è vero. Nel deserto più deserto possibile, la sabbia si riscalda e poi si raffredda emettendo un leggerissimo sibilo e una quantità di altrettanto flebili crick. E i deserti di ghiaccio sono ancora più rumorosi.
Bisogna andare fuori da qualsiasi atmosfera per trovare il silenzio, ma qui nemmeno la musica ha spazio. Il suono e quindi il non-silenzio è la condizione perché la musica esista.
Allora la musica non emerge dal silenzio, può solo emergere dalla non musica. Quindi la musica è suono organizzato, come affermava Varèse?
Forse, ma organizzato da chi? O da cosa? Il vento che soffia fra due montagne in una valle dimenticata o il disgelo della Dvina sentito dall’alto di una collina producono della musica coerente, che trova in sé stessa la propria giustificazione e arriva a degli estremi di dolcezza e di forza con cui le nostre composizioni non possono nemmeno competere…
Se ne è accorto perfino Bob Dylan:
Lay down your weary tune, lay down, Lay down the song you strum
And rest yourself ‘neath the strength of strings, No voice can hope to hum
The ocean wild like an organ played, The seaweed wove its strands
The crashing waves like cymbals clashed, Against the rocks and the sand